题目内容
10. 如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是34cm.
如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是34cm.
分析 展开后连接SF,求出SF的长就是捕获苍蝇充饥的蜘蛛所走的最短路径,过S作SE⊥CD于E,求出SE、EF,根据勾股定理求出SF即可.
解答 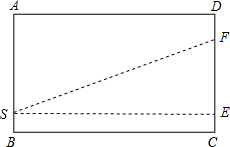 解:如图展开后连接SF,求出SF的长就是捕获苍蝇充饥的蜘蛛所走的最短路径,
解:如图展开后连接SF,求出SF的长就是捕获苍蝇充饥的蜘蛛所走的最短路径,
过S作SE⊥CD于E,
则SE=BC=$\frac{1}{2}$×60=30cm,
EF=18-1-1=16cm,
在Rt△FES中,由勾股定理得:SF=$\sqrt{S{E}^{2}+E{F}^{2}}$=$\sqrt{3{0}^{2}+1{6}^{2}}$=34(cm),
答:捕获苍蝇充饥的蜘蛛所走的最短路径的长度是34cm.
故答案为:34.
点评 本题考查了勾股定理、平面展开-最短路线问题,关键是构造直角三角形,题目比较典型,难度适中.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
20. 如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )
如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )
 如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )
如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.当x=( )时,分式$\frac{x-1}{x+1}$的值无意义.
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
2. 已知二次函数y=ax2+bx+c的图象如图所示,有下列4个结论,
已知二次函数y=ax2+bx+c的图象如图所示,有下列4个结论,
(1)abc>0;(2)b>a+c;(3)4a+2b+c>0;(4)b=-2a
其中正确的结论有( )
 已知二次函数y=ax2+bx+c的图象如图所示,有下列4个结论,
已知二次函数y=ax2+bx+c的图象如图所示,有下列4个结论,(1)abc>0;(2)b>a+c;(3)4a+2b+c>0;(4)b=-2a
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.下列变形正确的是( )
| A. | 4x-5=3x+2变形得4x-3x=-2+5 | B. | 3x=2变形得$x=\frac{3}{2}$ | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{2}{3}x-1=\frac{1}{2}x+3$变形得4x-6=3x+18 |
20.某班实行小组量化考核制.为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到数据制成如下的统计表:
(1)请根据表中的数据计算甲组与乙组的平均数、中位数、方差.(注:方差的计算结果精确到0.1)
(2)请你分别对甲、乙两个小组连续六周的学习情况作出简要评价.
| 一 | 二 | 三 | 四 | 五 | 六 | |
| 甲 | 12 | 15 | 16 | 14 | 14 | 13 |
| 乙 | 9 | 14 | 10 | 17 | 16 | 18 |
(2)请你分别对甲、乙两个小组连续六周的学习情况作出简要评价.
 如图所示,点B为DC中点,△AEF为等腰三角形.求证:DE=AC.
如图所示,点B为DC中点,△AEF为等腰三角形.求证:DE=AC. 如图,FE⊥AB于点E,AC⊥BF于点C,连结AF,EC,点M,N分别为AF,EC的中点,连结ME,MC.
如图,FE⊥AB于点E,AC⊥BF于点C,连结AF,EC,点M,N分别为AF,EC的中点,连结ME,MC. (1)四年一度的国际数学大会于2002年8月20日在北京召开.大会会标如图甲.它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若小正方形的面积为1,每个三角形两直角边的和是5.求大正方形的面积.
(1)四年一度的国际数学大会于2002年8月20日在北京召开.大会会标如图甲.它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若小正方形的面积为1,每个三角形两直角边的和是5.求大正方形的面积.