Question

如图，利用一面墙（墙的长度不超过45m），用80m长的篱笆围一个矩形场地.

（1）怎样围才能使矩形场地的面积为750m²？

（2）能否使所围矩形场地的面积为810 m²，为什么？

 

Answer 1

【答案】

（1）当所围矩形的长为30m、宽为25m时，能使矩形的面积为750m²；（2）不能．

【解析】

试题分析：（1）设所围矩形ABCD的长AB为x米，则宽AD为 米，根据矩形面积的计算方法列出方程求解；（2）假使矩形面积为810米，则方程无实数根，所以不能围成矩形场地．

试题解析：（1）设所围矩形ABCD的长AB为x米，则宽AD为米．

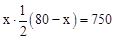依题意，得，即.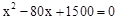

解此方程，得x₁=30，x₂=50.

∵墙的长度不超过45m，∴x₂=50不合题意，应舍去．

当x=30时，.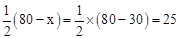

答：当所围矩形的长为30m、宽为25m时，能使矩形的面积为750m²．

（2）不能．理由如下：

由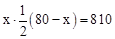得．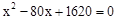

∵，

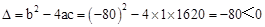∴方程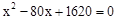没有实数根．

∴不能使所围矩形场地的面积为810m²．

考点：1.一元二次方程的应用（几何问题）；2. 矩形的性质；3.一元二次方程根的判别式.