题目内容
12. 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.(1)此变化过程中,时间是自变量,路程因变量;
(2)甲的速度是$\frac{50}{3}$千米/时,乙的速度是$\frac{100}{3}$千米/时;
(3)6时表示乙追上甲;
(4)路程为150千米,甲行驶了9小时,乙行驶了4小时;
(5)9时甲在乙的后面(前面、后面、相同位置);
(6)分别写出甲乙两人行驶的路程s(千米)与行驶的时间t(小时)的函数关系式(不要求写出自变量的取值范围)
S甲=$\frac{50}{3}$t
S乙=$\frac{150}{4}$t-$\frac{450}{4}$.
分析 (1)根据观察函数图象的横坐标、纵坐标,可得答案;
(2)根据观察纵坐标,可得路程,根据观察横坐标,可得时间,根据路程除以时间,可得答案;
(3)根据距离相等,可得答案;
(4)函数图象的纵坐标,可得答案;
(5)根据待定系数法,可得答案.
解答 解:(1)此变化过程中,时间是自变量,路程因变量;
(2)甲的速度是 $\frac{50}{3}$千米/时,乙的速度是 $\frac{100}{3}$千米/时;
(3)6时表示 乙追上甲;
(4)路程为150千米,甲行驶了 9小时,乙行驶了 4小时;
(5)9时甲在乙的 后面(前面、后面、相同位置);
(6)分别写出甲乙两人行驶的路程s(千米)与行驶的时间t(小时)的函数关系式(不要求写出自变量的取值范围)
S甲=$\frac{50}{3}$t
S乙=$\frac{100}{3}$t-100.
故答案为:(1)时间、路程;(2)50/3,100/3;(3)乙追上甲;(4)9,4;(5)后面;(6)S甲=$\frac{50}{3}$t;S乙=$\frac{100}{3}$t-100.
点评 本题考查了函数图象,观察函数图象的纵坐标得出距离,观察函数图象的横坐标得出时间,又利用了待定系数球函数解析式.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
20. 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
另外,一卡通普通卡刷卡实行5折优惠,学生卡刷卡实行2.5折优惠.
小明用学生卡乘车,上车时站名上对应的数字是5,下车时站名上对应的数字是22,那么,小明乘车的费用是1元.
 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:| 乘车路程计价区段 | 0-10 | 11-15 | 16-20 | … |
| 对应票价(元) | 2 | 3 | 4 | … |
小明用学生卡乘车,上车时站名上对应的数字是5,下车时站名上对应的数字是22,那么,小明乘车的费用是1元.
1.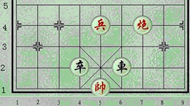 如图,若車的位置是(5,1),那么兵的位置可以记作( )
如图,若車的位置是(5,1),那么兵的位置可以记作( )
 如图,若車的位置是(5,1),那么兵的位置可以记作( )
如图,若車的位置是(5,1),那么兵的位置可以记作( )| A. | (1,5) | B. | (4,3) | C. | (3,4) | D. | (3,3) |
 如图,AB∥CD,∠1=105°,∠2=140°,则∠3=65°.
如图,AB∥CD,∠1=105°,∠2=140°,则∠3=65°. 如图,是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片,经测得FG=9cm,则这个剪出的图形的周长是98cm.
如图,是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片,经测得FG=9cm,则这个剪出的图形的周长是98cm.