Question

如图：?OBCD中，∠DOB=60°，OD=2，以OD为直径的⊙P经过点B，点N为BC边上任意一点（与点B、C不重合），过N作直线MN⊥x轴，垂足为A，交DC边于M．设OA=t，△OMN的面积为s．
（1）求点D的坐标；
（2）求s与t之间的函数关系式，并写出自变量t的取值范围；
（3）当s为

3

8

3

时，直线MN与⊙P是什么位置关系．

Answer 1

分析：利用圆内接三角形的性质得出∠DBO=90°，从而求出D的坐标；运用圆与直线的线切知识求出直线MN与⊙P的关系．

解答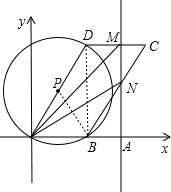：解：如下图所示：连接DB，BP

（1）由于⊙OP过点B，OD是圆的直径，所以∠DBO=90°
在Rt△OBD中，OB=OD×cos∠DOB=2×

1

2

=1；DB=OD×sin∠DOB=2×

3

2

=

3

所以点D的坐标为：D（1，

3

）；

（2）由于ODBC是平行四边形，且MN⊥x轴于A
所以AM=BD=

3

，∠CBA=∠DOB=60°
在Rt△BAN中，AN=tan∠CBA×BA=

3

（t-1）
所以MN=AM-AN=

3

（2-t）
即：△OMN的面积为s=

1

2

×MN×OA=

1

2

×

3

（2-t）t=

3

2

t（2-t）
又∵点N为BC边上与点B、C不重合的任意一点，
∴t的取值范围为：1＜t＜2；

（3）当s=

3

2

t（2-t）=

3 3

8

时，又1＜t＜2，所以t=

3

2

圆心P到MN的距离等于

1

2

（DM+OA）=

1

2

×（

3

2

-1+

3

2

）=1=

1

2

OD
所以此时直线MN与⊙P相切．

点评：本题考查圆内接三角形的性质和直线与圆相切的知识．