题目内容
4.先化简,再求值.(1)-2x3+4x-$\frac{1}{3}$x2-(x+3x2-2x3),其中x=3;
(2)$\frac{1}{2}$x-2(x-$\frac{1}{3}$y2)+(-$\frac{3}{2}$x+$\frac{1}{3}$y2),其中x=-2,y=-3.
分析 (1)原式去括号合并得到最简结果,把x的值代入计算即可求出值;
(2)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=-2x3+4x-$\frac{1}{3}$x2-x-3x2+2x3=-$\frac{10}{3}$x2+3x,
当x=3时,原式=-30+9=-21;
(2)原式=$\frac{1}{2}$x-2x+$\frac{2}{3}$y2-$\frac{3}{2}$x+$\frac{1}{3}$y2=-3x+y2,
当x=-2,y=-3时,原式=6+9=15.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
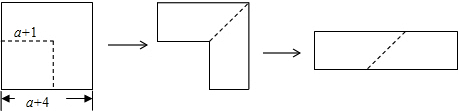

| A. | 3a+5 | B. | 6a+9 | C. | 2a2+5a | D. | 6a+15 |
 如图,数轴上的点A,B分别表示数-1和2,点C是线段AB的中点,则点C表示的数是0.5.
如图,数轴上的点A,B分别表示数-1和2,点C是线段AB的中点,则点C表示的数是0.5. 如图所示的几何体是由4个面围成,面与面相交成6条线.
如图所示的几何体是由4个面围成,面与面相交成6条线. 如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC=130°.
如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC=130°.