Question

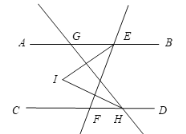
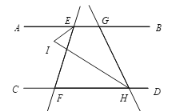
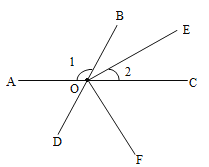
【题目】如图所示，点、、在同一直线上，是的平分线，，，.

（1）求的度数（请写出解题过程）.

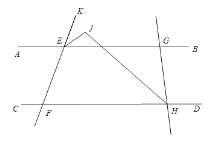
（2）如以为一边，在的外部画，问边与边成一直线吗？请说明理由.

Answer 1

【答案】（1）；（2）边与边成一直线，理由详见解析.

【解析】

（1）因为OE是∠BOC的平分线所以∠BOC=2∠2，再根据点A、O、C在一直线上，求出∠1和∠2关于x的关系式，列出等式求出x的值；
（2）根据∠EOF=∠EOC+∠COF=90°和∠EOC=∠BOC，∠FOC=∠DOC，∠BOC+∠DOC=90°，得出∠BOC+∠DOC=180°，进而可可判断边OD与边OB成一直线．

（1）因为是的平分线，所以，

因为点、、在同一直线上，所以，

又因为，，

所以，

解得：，

（2）边与边成一直线.

理由：因为，

又因为，.

∴，

即，所以点、、在同一直线上，即边与边成一直线.