��Ŀ����
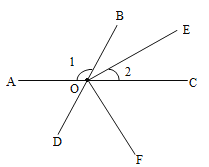
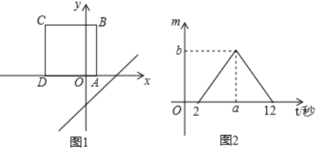
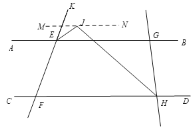
����Ŀ����ͼ1��ֱ��AB��CD��ֱ��EF��AB�ڵ�E����CD�ڵ�F����G�͵�H�ֱ���ֱ��AB��CD�ϵĶ��㣬��ֱ��GH��EIƽ����AEF��HIƽ����CHG��EI��HI���ڵ�I.
��1����ͼ����G�ڵ�E����࣬��H�ڵ�F���Ҳ࣬����AEF=70�㣬��CHG=60�㣬���ETH�Ķ���.
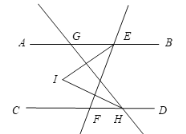
��2����ͼ����G�ڵ�E���Ҳ࣬��HҲ�ڵ�F���Ҳ࣬����AEF=![]() ����CHG=���������������䣬���ETH�Ķ���.
����CHG=���������������䣬���ETH�Ķ���.
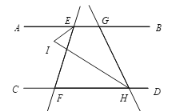
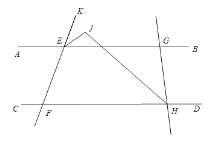
��3����ͼ����G�ڵ�E���Ҳ࣬��HҲ�ڵ�F���Ҳ࣬��GHC��ƽ����HJ����KEG��ƽ����EJ�ڵ�J.�����������䣬����AEF=![]() ����CHG=�������EJH�Ķ���.
����CHG=�������EJH�Ķ���.
���𰸡���1��65�㣻��2��![]() ����3��
����3��![]() .
.
��������
��1������I��IM��AB ���ɽ�ƽ���ߵ����ʵõ���AEI=35�㣬��CHI=30�㣬
����ƽ���ߵ����ʣ���IM��AB�õ���MIE=��AEI=35�㣬��AB��CD��IM��AB
�ɵá�MIH=��CHI=30�㣬���ɡ�EIH=��MIE+��MIH���㼴�ɵõ��𰸣�
��2������I��IM��AB���ɽ�ƽ���ߵ����ʵõ���AEI=![]() ����CHI=
����CHI=![]() ������ƽ���ߵ�������IM��AB�ɵá�MIE=��AEI=
������ƽ���ߵ�������IM��AB�ɵá�MIE=��AEI=![]() ����AB��CD��IM��AB�õ�IM��CD���������õ���EIH=��MIE+��MIH���㼴�ɵõ��𰸣�
����AB��CD��IM��AB�õ�IM��CD���������õ���EIH=��MIE+��MIH���㼴�ɵõ��𰸣�
��3������J��MN��AB ���ɽ�ƽ���ߵ����ʵõ���JEG=![]() ����JHF=
����JHF=![]() ������ƽ���ߵ�������MN��AB�õ���MJE=��JEG =
������ƽ���ߵ�������MN��AB�õ���MJE=��JEG =![]() ����AB��CD��MN��AB�õ�MN��CD���������õ���EJH=180��-��MJE-��NJH�����㼴�ɵõ���.
����AB��CD��MN��AB�õ�MN��CD���������õ���EJH=180��-��MJE-��NJH�����㼴�ɵõ���.
��1���⣺����I��IM��AB

��EIƽ�֡�AEF��HIƽ�֡�CHG����AEF=70�㣬��CHG=60�㣬
���AEI=35�㣬��CHI=30��
��IM��AB
���MIE=��AEI=35��
��AB��CD��IM��AB
��IM��CD
���MIH=��CHI=30��
���EIH=��MIE+��MIH=35��+30��=65��
��2���⣺����I��IM��AB

��EIƽ�֡�AEF��HIƽ�֡�CHG����AEF=![]() ����CHG=����
����CHG=����
���AEI=![]() ����CHI=
����CHI=![]()
��IM��AB
���MIE=��AEI=![]()
��AB��CD��IM��AB
��IM��CD
���MIH=��CHI=![]()
���EIH=��MIE+��MIH=![]() +
+![]()
��3���⣺����J��MN��AB
�ߡ�AEF=![]()
���KEB=![]()
��EJƽ�֡�KEB��HJƽ�֡�CHG����KEB =![]() ����CHG=����
����CHG=����
���JEG=![]() ����JHF=
����JHF=![]()
��MN��AB
���MJE=��JEG =![]()
��AB��CD��MN��AB
��MN��CD
���NJH=��CHJ=![]()
���EJH=180��-��MJE-��NJH=180��-![]() -
-![]() .
.