Question

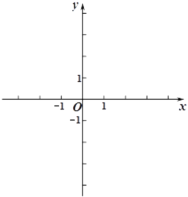
【题目】在平面直角坐标系中，关于的二次函数的图象过点，．

（1）求这个二次函数的表达式；

（2）求当时，的最大值与最小值的差；

（3）一次函数的图象与二次函数的图象交点的横坐标分别是和，且，求的取值范围．

Answer 1

【答案】（1）；（2）；（3）．

【解析】

（1）利用待定系数法将点，代入解析式中解方程组即可；

（2）根据（1）中函数关系式得到对称轴，从而知在中，当x=-2时，y有最大值，当时，y有最小值，求之相减即可；

（3）根据两函数相交可得出x与m的函数关系式，根据有两个交点可得出>0，根据根与系数的关系可得出a，b的值，然后根据，整理得出m的取值范围．

解：（1）∵的图象过点，，

∴

解得

∴

（2）由（1）得，二次函数对称轴为

∴当时，y的最大值为(-2)2-(-2)-2=4,

y的最小值为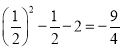

∴的最大值与最小值的差为；

（3）由题意及（1）得

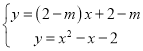
整理得

即

∵一次函数的图象与二次函数的图象交点的横坐标分别是和，

∴

化简得

即

解得m≠5

∴a，b为方程的两个解

又∵

∴a=-1，b=4-m

即4-m>3

∴m<1

综上所述，m的取值范围为．