题目内容
(满分11分)
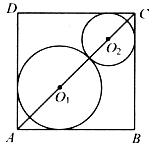
如图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H.

(1)证明:△ABG △ADE ;
(2)试猜想BHD的度数,并说明理由;
(3)将图中正方形ABCD绕点A逆时针旋转(0°<BAE <180°),设△ABE的面积为
,△ADG的面积为
,判断
与
的大小关系,并给予证明.
略
解析:(1)证法一:
证明:在正方形ABCD和正方形AEFG中
∠GAE=∠BAD=90° ……1分
∠GAE+∠EAB=∠BAD+EAB
即∠GAB=∠EAD ……2分
又AG=AE AB=AD
∴△ABG≌△ADE ……4分
证法二:
证明:因为四边形ABCD与四边形AEFG都是正方形,所以∠GAE=∠BAD=90°,AG=AE,AB=AD,所以△EAD可以看成是△GAB逆时针旋转90°得到,
所以△ABG≌△ADE
(2)证法一:
我猜想∠BHD=90°理由如下:
∵△ABG≌△ADE ∴∠1=∠2 ……5分
而∠3=∠4 ∴∠1+∠3=∠2+∠4
∵∠2+∠4=90 ∠1+∠3=90° ……6分
∴∠BHD=90° ……7分
证法二:
我猜想∠BHD=90°理由如下:
由(1)证法(二)可知△EAD可以看成是△GAB逆时针旋转90°得到,BG与DE是一组对应边,
所以BG⊥DE,即∠BHD=90°
(3)证法一:
当正方形ABCD绕点A逆时针旋转
0°<∠BAE<180°时,S1和S2总保持相等. ……8分
证明如下:由于0°<∠BAE<180°因此分三种情况:
①当0°<∠BAE<90°时 (如图10)
过点B作BM⊥直线AE于点M,
过点D作DN⊥直线AG于点N.

∵∠MAN=∠BAD=90°
∴∠MAB=∠NAD
又∠AMB=∠AND=90° AB=AD
∴△AMB≌△AND
∴BM=DN 又AE=AG
∴
∴ ……9分
②当∠BAE=90°时如图10()
∵AE=AG ∠BAE =∠DAG =90°AB=AD
∴△ABE≌△ADG


∴ ……10分
③当90°<∠BAE<180°时 如图10(b)
和①一样;同理可证
综上所述,在(3)的条件下,总有. ……11分
证法二:
①当0°<∠BAE<90°时,如图10(c)
作EM⊥AB于点M,作GN⊥AD交DA延长线于点N,
则∠GNA=∠EMA=90°
又∵四边形ABCD与
四边形AEFG都是正方形,
∴AG=AE,AB=AD
∴∠GAN+∠EAN=90°,
∠EAM+∠EAN=90°
∴∠GAN=∠EAM
∴△GAN≌△EAM(AAS)∴GN=EM
∴
②③同证法一类似
证法三:
当正方形ABCD绕点A逆时针旋转0°<∠BAE<180°时,S1和S2总保持相等. ……8分

证明如下:由于0°<∠BAE<180°因此分三种情况:
①当0°<∠BAE<90°时 如图10(d)
延长GA至M使AM=AG,连接DM,则有
∵AE=AG=AM,AB=AD
又∠1+∠2=90°
∠3+∠2=90°
∴∠1=∠3
∴△ABE≌△ADM (SAS)
∴
∴ ……9分
②当∠BAE=90°时(同证法一) ……10分
③当90°<∠BAE<180°时如图10(e)和①一样;
同理可证
综上所述,在(3)的条件下,总有 ……11分

证法四:
当0°<∠BAE<90°时如图10(f)延长DA至M使AM=AD,连接GM,

则有
再通过证明
△ABE与△AMG全等从而证出 ②③同证法一类似
证法五:
(这种证法用三角函数知识证明,无须分类证明)
如图10(g)四边形ABCD与四边形AEFG都是正方形,

∴AG=AE,AB=AD
当∠BAE=时,∠GAD=180°-
则
sin(180°-)=sin
即
∴


 经过坐标原点O和x轴上另一点E(4,0)
经过坐标原点O和x轴上另一点E(4,0) 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;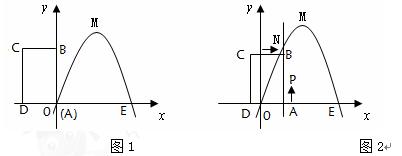
 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.

 ,
, .
.