题目内容
（1）已知关于x的一元二次方程2x2-8nx+10x-n2+35n-76=0（n为自然数）的两根都为质数，求此方程的两根．
（2）已知x-3x+1=0，求
的值．
解：（1）由于两根之和为4n-5是一个奇数，而两根都是质数，所以必有一根是2，
把2代入方程，得8-16n+20-n2+35n-76=0，
即n2-19n+48=0，
解得n=3或16，
当n=3时，原方程为2x2-14x+20=0，此时两根为2和5；
当n=16时，原方程为2x2-118x+228=0，此时两根为2和57．
即此方程的三根为2、5、57．
（2）∵x-3x+1=0，
∴x=
所以=
=
．
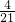分析：（1）首先根据两根之和和两根为质数得到一个根是2，将2代入可求到n的值，从而得到方程的解；
（2）由x-3x+1=0得到x的值，然后代入分式，化简求值．
点评：本题主要考查了根与系数的关系和分式的化简求值，同时还有质数的有关性质．
把2代入方程，得8-16n+20-n2+35n-76=0，
即n2-19n+48=0，
解得n=3或16，
当n=3时，原方程为2x2-14x+20=0，此时两根为2和5；
当n=16时，原方程为2x2-118x+228=0，此时两根为2和57．
即此方程的三根为2、5、57．
（2）∵x-3x+1=0，
∴x=
所以
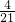==．分析：（1）首先根据两根之和和两根为质数得到一个根是2，将2代入可求到n的值，从而得到方程的解；
（2）由x-3x+1=0得到x的值，然后代入分式，化简求值．
点评：本题主要考查了根与系数的关系和分式的化简求值，同时还有质数的有关性质．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目