题目内容
13.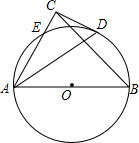 如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CE=2,CD=4.
如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CE=2,CD=4.(1)求点D到AB的距离;
(2)求⊙O的半径R及BC的长.
分析 (1)连接OD,由直线CD与⊙O相切于点C,AD⊥CD,易证得OC∥AD,继而可得AC平分∠DAB,根据角平分线的性质即可得到结论;
(2)过O作AC的垂线,设垂足为G,得到四边形ODCG是矩形,根据切割线定理得到CD2=CE•CA,求得AC=8,AE=6,GE=$\frac{1}{2}$AE=3,于是得到⊙O的半径=5,连接BE,由AB是⊙O的直径,得到∠AEB=90°,根据勾股定理得到BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=8,BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=2$\sqrt{17}$.
解答 解:(1)连接OD, ∵CD与⊙O相切于点D,
∵CD与⊙O相切于点D,
∴OD⊥CD,
∵AC⊥CD,
∴OD∥AD,
∴∠DAC=∠ODA,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,
即AD平分∠CAB,
∴点D到AB的距离=CD=4;
(2)过O作AC的垂线,设垂足为G,
∵∠C=90°,
∴∠C=∠OGC=∠ODC=90°,
∴四边形ODCG是矩形,
∵CD是切线,CEA是割线,
∴CD2=CE•CA,
∵CD=2CE=4,
∴AC=8,
∴AE=6,
∴GE=$\frac{1}{2}$AE=3,
∴OD=CG=EG+EC=3+2=5,
∴⊙O的半径=5,
连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∵AB=OD=10,AE=6,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=8,
∵CE=2,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=2$\sqrt{17}$.
点评 此题考查了切线的性质,矩形的判定与性质,垂径定理,以及切割线定理,其中作出相应的辅助线是解本题的关键.

练习册系列答案
相关题目
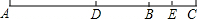 如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E是BC的中点.
如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E是BC的中点. 如图,
如图,