题目内容
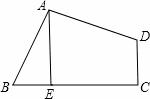
如图，矩形ABCD中，AD=
，F是DA延长线上一点，G是CF上一点，且∠ACG=∠AGC，∠GAF=∠F=20°，则AB= ．
.
【解析】由三角形的外角性质得，∠AGC=∠GAF+∠F=20°+20°=40°，
∵∠ACG=∠AGC，∴∠CAG=180°-∠ACG-∠AGC=180°-2×40°=100°，
∴∠CAF=∠CAG+∠GAF=100°+20°=120°，∴∠BAC=∠CAF-∠BAF=30°
，
在Rt△ABC中，AC=2BC=2AD=2，
由勾股定理，AB=
．
练习册系列答案
名校课堂系列答案
相关题目
，点A是⊙O上一点，且AB=AC，直线AO与BC交于点D，则AD的长为 ．
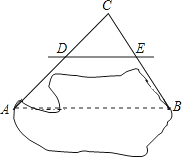
=0，那么菱形的面积等于 ．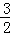
，0），且与反比例函数y=
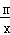（m≠0）的图象相交于点A（﹣2，1）和点B．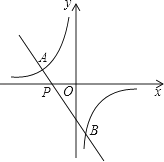
） D1（ ， ）