Question

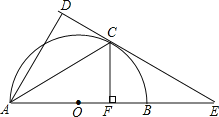
【题目】如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4．若动点D在线段AC上（不与点A、C重合），过点D作DE⊥AC交AB边于点E．点A关于点D的对称点为点F，以FC为半径作⊙C，当DE=_______时，⊙C与直线AB相切．

Answer 1

【答案】或

【解析】

求出AB上的高，CH，即可得出圆的半径，证△ADE∽△ACB得出比例式，代入求出即可．

过C作CH⊥AB于H，

∵∠ACB=90°，BC=2，AB=4，AC=6，

∴由三角形面积公式得：BCAC=ABCH，

CH=3，

分为两种情况：①如图，

∵CF=CH=3，

∴AF=6-3=3，

∵A和F关于D对称，

∴DF=AD=，

∵DE∥BC，

∴△ADE∽△ACB，

∴，

∴，

DE=；

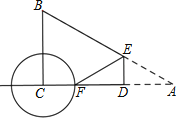
②如图2，

∵CF=CH=3，

∴AF=6+3=9，

∵A和F关于D对称，

∴DF=AD=4.5，

∵DE∥BC，

∴△ADE∽△ACB，

∴，

∴，

DE=.