题目内容

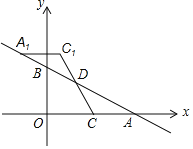
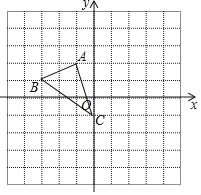
【题目】如图所示，在平面直角坐标系中有一格点三角形，该三角形的三个顶点为：A（1，1），B（-3，1），C（-3，-1）．

（1）若△ABC的外接圆的圆心为P，则点P的坐标为 ，⊙P的半径为 ；

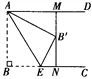
（2）如图所示，在11×8的网格图内，以坐标原点O点为位似中心，将△ABC按相似比2：1放大，A、B、C的对应点分别为A'、B'、C'．

①画出△A'B'C'；

②将△A'B'C'沿x轴方向平移，需平移 个单位长度，能使得B'C'所在的直线与⊙P相切．

【答案】（1）（-1，0）；；（2）①作图见解析；②5-或5+．

【解析】

（1）由题意可知△ABC是直角三角形，作出外接圆即可；

（2）利用位似图形的定义和性质作出图形，再根据平移的定义和性质及切线的判定即可得平移的距离．

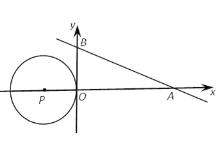
（1）△ABC的外接圆⊙P如图所示

由图可知，点P的坐标为（-1，0）、半径为；

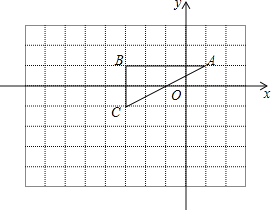
（2）①如图所示，△A′B′C′即为所求．

②将△A′B′C′向右平移5-或5+个单位B′C′所在的直线与⊙P相切，

故答案为：5-或5+．

练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4．若动点D在线段AC上（不与点A、C重合），过点D作DE⊥AC交AB边于点E．点A关于点D的对称点为点F，以FC为半径作⊙C，当DE=_______时，⊙C与直线AB相切．

【题目】如图，在△ABC中，中线BE，CD相交于点O，连接DE，下列结论： ①=； ②=；③=；④=.其中正确的个数有（ ）

A. 1个 B. 2个 C. 3个 D. 4个

【题目】如图，抛物线 y＝﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点（点 A 在点 B 的左边），与 y轴交于点 C，点 D 为抛物线的顶点．

（1）求点 A、B、C 的坐标；

（2）点 M（m，0）为线段 AB 上一点（点 M 不与点 A、B 重合），过点 M 作 x 轴的垂线，与直线 AC 交于点 E，与抛物线交于点 P，过点 P 作 PQ∥AB 交抛物线于点 Q，过点 Q 作 QN⊥x 轴于点 N，可得矩形 PQNM．如图，点 P 在点 Q 左边，试用含 m 的式子表示矩形 PQNM 的周长；

（3）当矩形 PQNM 的周长最大时，m 的值是多少？并求出此时的△AEM 的面积；

（4）在（3）的条件下，当矩形 PMNQ 的周长最大时，连接 DQ，过抛物线上一点 F 作 y 轴的平行线，与直线 AC 交于点 G（点 G 在点 F 的上方）．若 FG＝2DQ，求点 F 的坐标．

【题目】（定义）如图1，A，B为直线l同侧的两点，过点A作直线l的对称点，连接B交直线l于点P，连接AP，则称点P为点A，B关于直线的“等角点”．

（运用）如图2，在平面直坐标系xOy中，已知A(2,)，B(-2,-)两点．

（1）C(4,)，D(4,)，E(4,)三点中，点　　是点A，B关于直线x=4的等角点；

（2）若直线l垂直于x轴，点P(m,n)是点A，B关于直线l的等角点，其中m>2，∠APB=α，求证：；

（3）若点P是点A，B关于直线y=ax+b(a≠0)的等角点，且点P位于直线AB的右下方，当∠APB=60°时，求b的取值范围（直接写出结果）．

【题目】如图，一次函数y=-x+m（m＞0）的图象与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D.

（1）若点C1恰好落在y轴上，试求的值；

（2）当n=4时，若△A1C1D被y轴分得两部分图形的面积比为3：5，求该一次函数的解析式．

【题目】如图，已知△ABC．

（1）求AC的长；

（2）先将△ABC向右平移2个单位得到△A′B′C′，写出A点的对应点A′的坐标；

（3）再将△ABC绕点C按逆时针方向旋转90°后得到△A1B1C1，写出A点对应点A1的坐标．

（4）求点A到A′所画过痕迹的长．

【题目】如图，已知AD∥BC,AB⊥BC，AB=3.点E为射线 BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于点M，N.当点B′为线段MN的三等分点时，BE的长为__________ .

【题目】如图，直线y＝－x＋2 与x轴、y轴分别相交于A、B两点，圆心P的坐标为（－2，0），⊙P与y轴相切于点O．若将⊙P沿x轴向右移动，当⊙P与该直线相交时，满足横坐标为整数的点P的个数是（ ）

A. 3 B. 4 C. 5 D. 7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网