题目内容
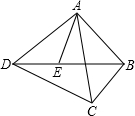如图，点E是四边形ABCD的对角线BD上的一点，且∠BAC=∠BDC=∠DAE．（1）试说明：BE•AD=CD•AE；
（2）根据图形的特点，猜想
| BC | DE |
分析：（1）通过证明∠EAB=∠DAC，∠AEB=∠ADC，得出△ADC∽△AEB，得出结论．
（2）证明△BAC∽△EAD，得出结论．
（2）证明△BAC∽△EAD，得出结论．
解答：（1）证明：∵∠BAC=∠DAE，
∴∠BAC+∠EAC=∠DAE+∠EAC．
∴∠EAB=∠DAC①；
又∵∠AEB=∠DAE+∠BDA=∠BDC+∠BDA，
∴∠AEB=∠ADC②；
由①和②得△AEB∽△ADC．
∴
=
∴BE•AD=CD•AE．
（2）猜想：
=
或
=
．
证明：∵△AEB∽△ADC，
∴
=
．
∵∠BAC=∠DAE，
∴△BAC∽△EAD．
∴
=
=
．
∴∠BAC+∠EAC=∠DAE+∠EAC．
∴∠EAB=∠DAC①；
又∵∠AEB=∠DAE+∠BDA=∠BDC+∠BDA，
∴∠AEB=∠ADC②；
由①和②得△AEB∽△ADC．
∴
| BE |
| DC |
| AE |
| AD |
（2）猜想：
| BC |
| DE |
| AC |
| AD |
| BC |
| DE |
| AB |
| AE |
证明：∵△AEB∽△ADC，
∴
| AB |
| AE |
| AC |
| AD |
∵∠BAC=∠DAE，
∴△BAC∽△EAD．
∴
| BC |
| ED |
| AC |
| AD |
| AB |
| AE |
点评：通过将乘积的形式转化成比例的形式，本题考查了相似三角形的判定和性质．
练习册系列答案
名校课堂系列答案
相关题目
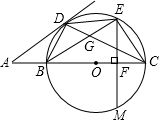EF⊥BC于点F，交⊙O于点M，EM=
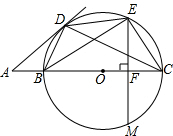B=∠DEB，EF⊥BC于点F，交⊙O于点M，EM=2
如图，点P是四边形ABCD内一点，分别在边AB、BC上作出点M，点N，使PM+PN的值最小，保留作图痕迹，不写作法．
如图，点O是四边形ABCD与A′B′C′D′的位似中心，则