题目内容
已知:如图,点O是四边形BCED外接圆的圆心,点O在BC上,点A在CB的延长线上,且∠AD B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2
B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2| 5 |
(1)求证:AD是⊙O的切线;
(2)若弧BM上有一动点P,且sin∠CPM=
| 2 |
| 3 |
(3)在(2)的条件下,如果DE=
| 14 |
分析:(1)连接OD,由BC是⊙O的直径,根据圆周角定理的推论得到∠BDC=90°,而∠CBD=∠ODB,∠DEB=∠BCD,则∠ADB+∠ODB=90°,即可得到结论;
(2)根据圆周角定理得到∠CPM=∠CEM,则sin∠CEM=sin∠CPM=
=
,设FC=2k,则EC=3k,EF=
k,根据垂径定理得EF=
,弧EC=弧MC.则k=1,FC=2,EC=3;再由圆周角定理的推论得到∠BEC=90°,sin∠EBC=sinP=
=
,即可求出BC;
(3)作直径EQ,连接DQ.根据圆周角定理的推论得∠QDE=90°,在Rt△DEQ中利用勾股定理求出DQ,而∠DBE=∠Q,然后利用正切的定义计算即可.
(2)根据圆周角定理得到∠CPM=∠CEM,则sin∠CEM=sin∠CPM=
| FC |
| EC |
| 2 |
| 3 |
| 5 |
| 5 |
| EC |
| BC |
| 2 |
| 3 |
(3)作直径EQ,连接DQ.根据圆周角定理的推论得∠QDE=90°,在Rt△DEQ中利用勾股定理求出DQ,而∠DBE=∠Q,然后利用正切的定义计算即可.
解答: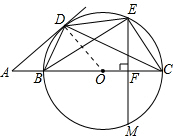 (1)证明:连接OD,
(1)证明:连接OD,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠BCD+∠CBD=90°.
又∵OD=OB,
∴∠CBD=∠ODB.
∴∠BCD+∠ODB=90°.
∵∠ADB=∠DEB,
而∠DEB=∠BCD,
∴∠ADB=∠BCD.
∴∠ADB+∠ODB=90°.
∴AD是⊙O的切线;
(2)解:∵∠CPM=∠CEM,
∴sin∠CEM=sin∠CPM=
=
,
设FC=2k,则EC=3k,EF=
k,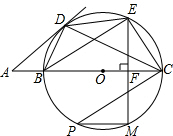
∵EM与直径BC垂直,且EM=2
,
∴EF=
,弧EC=弧MC.
∴k=1,FC=2,EC=3,∠EBC=∠P.
∵BC是⊙O的直径,
∴∠BEC=90°,
∴sin∠EBC=sin∠CPM=
=
,
∴BC=
,
即⊙O直径为
;
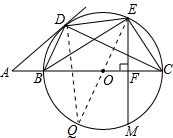
(3)作直径EQ,连接DQ.
∴∠QDE=90°,EQ=
,
在Rt△DEQ中,DQ=
=
.
∵∠DBE=∠Q,
∴tan∠DBE=tan∠Q=
=
.
 (1)证明:连接OD,
(1)证明:连接OD,∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠BCD+∠CBD=90°.
又∵OD=OB,
∴∠CBD=∠ODB.
∴∠BCD+∠ODB=90°.
∵∠ADB=∠DEB,
而∠DEB=∠BCD,
∴∠ADB=∠BCD.
∴∠ADB+∠ODB=90°.
∴AD是⊙O的切线;
(2)解:∵∠CPM=∠CEM,
∴sin∠CEM=sin∠CPM=
| FC |
| EC |
| 2 |
| 3 |
设FC=2k,则EC=3k,EF=
| 5 |

∵EM与直径BC垂直,且EM=2
| 5 |
∴EF=
| 5 |
∴k=1,FC=2,EC=3,∠EBC=∠P.
∵BC是⊙O的直径,
∴∠BEC=90°,
∴sin∠EBC=sin∠CPM=
| EC |
| BC |
| 2 |
| 3 |
∴BC=
| 9 |
| 2 |
即⊙O直径为
| 9 |
| 2 |

(3)作直径EQ,连接DQ.
∴∠QDE=90°,EQ=
| 9 |
| 2 |
在Rt△DEQ中,DQ=
| EQ2-DE2 |
| 5 |
| 2 |
∵∠DBE=∠Q,
∴tan∠DBE=tan∠Q=
| ||
|
2
| ||
| 5 |
点评:本题考查了切线的判定:过半径的外端点与半径垂直的直线为圆的切线.也考查了垂径定理、圆周角定理及其推论、勾股定理以及解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
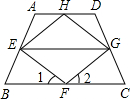 已知:如图,点E、F、G、H分别是梯形ABCD四条边上的中点,AD∥BC,AB=CD=EG=4.
已知:如图,点E、F、G、H分别是梯形ABCD四条边上的中点,AD∥BC,AB=CD=EG=4.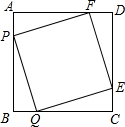 已知:如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
已知:如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.