题目内容
如图，第一象限内一点A，已知OA=s，OA与x轴正半轴所成的夹角为α，且tanα=2，那么点A的坐标是________．
（
，
）
分析：作AB⊥x轴于点B，利用角α的正切设出AB和OB的长，然后利用勾股定理分别求得AB和OB的长后即可表示出点A的坐标．
解答：
解：作AB⊥x轴于点B，
∵tanα=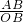
=2，
∴设OB=x，则AB=2x
在Rt△ABC中OB2+AB2=OA2，
即：5x2=s2
解得：x=
∴2x=
∴点A的坐标为（，），
故答案为：（，）．
点评：本题考查了解直角三角形及坐标与图形性质的知识，解题的关键是正确的构造直角三角形．
，）分析：作AB⊥x轴于点B，利用角α的正切设出AB和OB的长，然后利用勾股定理分别求得AB和OB的长后即可表示出点A的坐标．
解答：
解：作AB⊥x轴于点B，∵tanα=
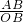=2，∴设OB=x，则AB=2x
在Rt△ABC中OB2+AB2=OA2，
即：5x2=s2
解得：x=
∴2x=
∴点A的坐标为（
，），故答案为：（
，）．点评：本题考查了解直角三角形及坐标与图形性质的知识，解题的关键是正确的构造直角三角形．
练习册系列答案
寒假学与练系列答案
相关题目
接EB并延长交x轴于点F．
y轴于E，点C为直线y=x上在第一象限内一点．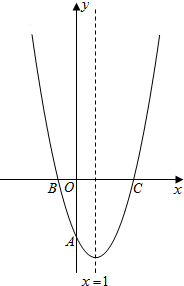
（2012•湘西州）如图，抛物线y=x2-2x+c与y轴交于点A（0，-3），与x轴交于B、C两点，且抛物线的对称轴方程为x=1．
如图，第一象限内一点A，已知OA=s，OA与x轴正半轴所成的夹角为α，且tanα=2，那么点A的坐标是