题目内容
⊙O和⊙O′的半径分别为R和R′，圆心距OO′=5，R=3，当0＜R′＜2时，⊙O和⊙O′的位置关系是
- A.内含
- B.外切
- C.相交
- D.外离
D
分析：两圆的位置关系与数量之间的联系：（P表示圆心距，R，r分别表示两圆的半径）
外离，则P＞R+r；外切，则P=R+r；相交，则R-r＜P＜R+r；内切，则P=R-r；内含，则P＜R-r．
解答：∵当R=3，0＜R′＜2时，
∴3＜R+R′＜5，
∴两圆外离．
故选D．
点评：本题主要考查两圆的位置关系与数量之间的联系．
分析：两圆的位置关系与数量之间的联系：（P表示圆心距，R，r分别表示两圆的半径）
外离，则P＞R+r；外切，则P=R+r；相交，则R-r＜P＜R+r；内切，则P=R-r；内含，则P＜R-r．
解答：∵当R=3，0＜R′＜2时，
∴3＜R+R′＜5，
∴两圆外离．
故选D．
点评：本题主要考查两圆的位置关系与数量之间的联系．
练习册系列答案
相关题目
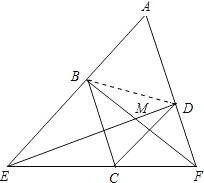如图，边长为a的菱形ABCD中，∠A=60°，过C任作直线分别交AB、AD的延长线于E、F，连接DE、BF交于M，若△BEM和△DFM外接圆的半径分别是R1、R2，求证：R1•R2为定值，并求这个定值．
