题目内容
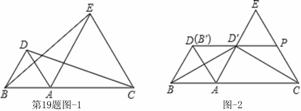
如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺 时针旋转得到△AB′D′.
时针旋转得到△AB′D′.
①当旋转角为 度时,边AD′落在AE上;
②在①的条件下,延长DD′交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.
 |
(1)证明:∵△ABD和△ACE都是等边三角形 ∴AB=AD,AE=AC,∠BAD=∠CAE=60°
∴∠BAD+∠DAE=∠CAE+∠DAE 即∠BAE=∠DAC
在△BAE和△DAC中,
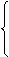 AB=AD
AB=AD
∠BAE=∠DAC
AE=AC,
∴△BAE≌△DAC(SAS) ∴BE=CD ------(3分)
(2)解:①∵∠BAD=∠CAE=60° ∴∠DAE=180°-60°×2=60°
∵边AD′落在AE上, ∴旋转角=∠DAE=60° ------(2分)
②当AC=2AB时,△BDD′与△CPD′全等.理由如下:
由旋转可知,AB′与AD重合 ∴AB=BD=DD′=AD′ ∴四边形ABDD′是菱形
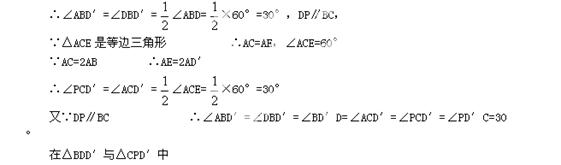
 ∠DBD′=∠PCD′
∠DBD′=∠PCD′
BD′=CD′
∠BD′D=∠PD′C,
∴△BDD′≌△CPD′(ASA) ------(3分)

练习册系列答案
相关题目
下列四个实数中,绝对值最小的数是
|
| A. | ﹣5 | B. |
| C. | 1 | D. | 4 |
 .
. 的解集是( )
的解集是( ) <-2 B.
<-2 B.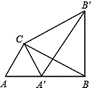

 ,-π,0.1235,
,-π,0.1235, 的六张卡片中,随机抽取一张,是无理数的概率为
的六张卡片中,随机抽取一张,是无理数的概率为 B.
B.  C.
C. D.1
D.1  的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.