题目内容
如图，以△ABC的边AB为直径作⊙O，交BC于点D，且∠DAC=∠B．
（1）求证：AC是⊙O的切线；
（2）若点E是
的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．
 |
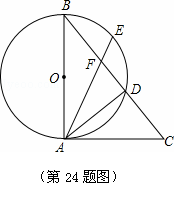解：（1）∵AB是⊙O的直径，∴∠ADB=∠ADC=90°.∵∠B=∠CAD，∠C=∠C，∴△ADC∽△BAC.
∴∠BAC=∠ADC=90°.∴BA⊥AC.∴AC是⊙O的切线．
（2）∵△ADC∽△BAC（已证），∴
=
，即AC2=BC×CD=3
6.解得：AC=6.
在Rt△ACD中，AD=
=2
.
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD，∴CA=CF=6，∴DF=CA﹣CD=2，
在Rt△AFD中，AF=
=2
．
练习册系列答案
阅读快车系列答案
相关题目
b＝（－2×3）
时针旋转得到△AB′D′．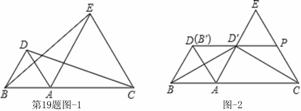
中，自变量x的取值范围是 .
示的整数是（ ）
