题目内容
 已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.
已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.(1)求证:BC是⊙P的切线;
(2)若CD=2,CB=2
| 2 |
分析:(1)连接PA,PB,根据圆内接四边形对角互补证明∠PBC是直角,从而可以确定CB是⊙P的切线;
(2)根据△FCE∽△PCB,则
=
,由于CB是⊙P的切线,所以根据CB2=CD•(CD+DE),可以求得DE的长度,进而求得CE的长度;再求得BP的长度即可,在Rt△CPB中,CP=3,CB=2,则可求得EF的长度.
(2)根据△FCE∽△PCB,则
| CB |
| CE |
| BP |
| EF |
解答:解:(1)连接PB,PA,
∵点P在⊙O上,
∵⊙O的弦AC切⊙P于点A,
∴∠CAP=90°,
∵四边形APBC是⊙O的内接四边形,
∴∠PBC=90°,即PB⊥CB.
∵B在⊙P上,
∴CB是⊙P的切线.
(2)∵CB是⊙P的切线,
∴CB2=CD•(CD+DE).
∵CD=2,CB=2
,
∴(2
)2═2×(2+ED).
∴DE=2.
∴CE=CD+DE=2+2=4.
∴在⊙P中,PD=PE=
ED=1,
∵CP=3,CB=2
,
∴BP=1.
∵EF⊥CE,
∴∠FEC=∠CBP=90°,∠FCE=∠PCB.
∴△FCE∽△PCB.
∴
=
,
∵CB=2
,CE=4,BP=1,
∴
=
,
∴EF=
.
∵点P在⊙O上,
∵⊙O的弦AC切⊙P于点A,

∴∠CAP=90°,
∵四边形APBC是⊙O的内接四边形,
∴∠PBC=90°,即PB⊥CB.
∵B在⊙P上,
∴CB是⊙P的切线.
(2)∵CB是⊙P的切线,
∴CB2=CD•(CD+DE).
∵CD=2,CB=2
| 2 |
∴(2
| 2 |
∴DE=2.
∴CE=CD+DE=2+2=4.
∴在⊙P中,PD=PE=
| 1 |
| 2 |
∵CP=3,CB=2
| 2 |
∴BP=1.
∵EF⊥CE,
∴∠FEC=∠CBP=90°,∠FCE=∠PCB.
∴△FCE∽△PCB.
∴
| CB |
| CE |
| BP |
| EF |
∵CB=2
| 2 |
∴
2
| ||
| 4 |
| 1 |
| EF |
∴EF=
| 2 |
点评:本题考查的是相交两圆的性质、切线的判定和切线的性质以及相似三角形的判定和相似三角形的性质,题目的综合性不小,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.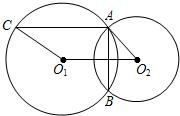 ,⊙O2的半径为
,⊙O2的半径为 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.