题目内容
16.若关于x的方程x2+2(k-1)x+k2=0有实数根,则k的取值范围是k≤$\frac{1}{2}$.分析 根据方程有实数根结合根的判别式即可得出△=-8k+4≥0,解之即可得出结论.
解答 解:∵关于x的方程x2+2(k-1)x+k2=0有实数根,
∴△=[2(k-1)]2-4k2=-8k+4≥0,
解得:k≤$\frac{1}{2}$.
故答案为:k≤$\frac{1}{2}$.
点评 本题考查了根的判别式,熟练掌握“当△≥0时一元二次方程有实数根”是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.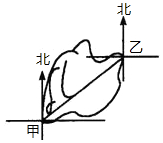 如图,甲、乙两地之间是一座山,现准备修一条隧道,在甲地测得隧道在北偏东50°的方向上,如果甲、乙两地同时开工,那么在乙地应按( )方向施工才能使隧道准确接通.
如图,甲、乙两地之间是一座山,现准备修一条隧道,在甲地测得隧道在北偏东50°的方向上,如果甲、乙两地同时开工,那么在乙地应按( )方向施工才能使隧道准确接通.
 如图,甲、乙两地之间是一座山,现准备修一条隧道,在甲地测得隧道在北偏东50°的方向上,如果甲、乙两地同时开工,那么在乙地应按( )方向施工才能使隧道准确接通.
如图,甲、乙两地之间是一座山,现准备修一条隧道,在甲地测得隧道在北偏东50°的方向上,如果甲、乙两地同时开工,那么在乙地应按( )方向施工才能使隧道准确接通.| A. | 南偏西50° | B. | 南偏西40° | C. | 东偏南50° | D. | 西偏南50° |
1.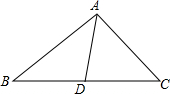 如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
 如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )| A. | 3 | B. | 10 | C. | 17 | D. | 20 |
5.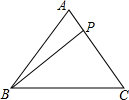 如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
 如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )| A. | 4.8 | B. | 8 | C. | 8.8 | D. | 9.8 |
 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是$\sqrt{7}$.
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是$\sqrt{7}$.