题目内容
已知，△ABC是等边三角形，点M是射线BC上任意一点，点N是射线CA上的任意一点，且BM＝CN．直线BN与AM相交于点Q，就下面图中给出的三种情况(如图①②③)，然后分别测量∠BQM的大小，由此猜测∠BQM的度数？并利用图③证明你的结论．
答案：
解析：
解析：
|
∠BQM＝60°． 证明：图③中， 在△ABM与△BCN中 ∴△ABM≌△BCN ∴∠M＝∠N ∵∠M＋∠MAC＝60°， ∴∠N＋∠NAQ＝60° ∴∠BQM＝60°． |
练习册系列答案
相关题目
某“研究性学习小组”遇到了以下问题，请参与：
已知，△ABC是等边三角形且内接于⊙O，取
上异于A、B的点M．设直线CA与BM相交于点K，直线CB与AM相交于点N．
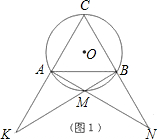
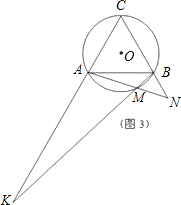
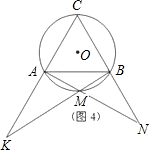
（1）如图1，图2，图3，M分别为
的中点、三分之一点、四分之一点，△ABC的边长均为2，分别测量出AK、BN的长，计算AK•BN的值（精确到0.01）并将结果填入下表中：
（2）如图4，当M为
上任意一点时，根据（1）的结果，猜想AK•BN与AB的数量关系式为 ；
（3）对（2）中提出的猜想，依图4给出证明．
已知，△ABC是等边三角形且内接于⊙O，取
 |
| AB |
（1）如图1，图2，图3，M分别为
|
| AB |
| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
|
| AB |
（3）对（2）中提出的猜想，依图4给出证明．
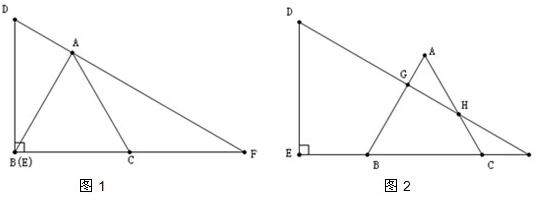
三个为条件，余下的一个为结论，组成一个正确的命题（只需写出一种），并给予证明．
