题目内容
如图(1),在等边的顶点B、C处各有一只蜗牛,它们同时出发△ABC分别以每分钟1各单位的速度油B向C和由C向A爬行,其中一只蜗牛爬到终点s时,另一只也停止运动,经过t分钟后,它们分别爬行到D,P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?为什么?
(2)问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化?请证明你的结论.
(3)若蜗牛沿着BC和CA的延长线爬行,BD与AP交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中的∠DQA大小变化了吗?若无变化,请证明.若有变化,请直接写出∠DQA的度数.
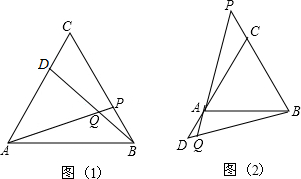
(1)在爬行过程中,BD和AP始终相等吗?为什么?
(2)问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化?请证明你的结论.
(3)若蜗牛沿着BC和CA的延长线爬行,BD与AP交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中的∠DQA大小变化了吗?若无变化,请证明.若有变化,请直接写出∠DQA的度数.

分析:(1)根据等边三角形性质得出∠CAB=∠C=∠ABP=60°,AB=BC,根据SAS推出△BDC≌△APB即可.
(2)根据△BDC≌△APB得出∠CBD=∠BAP,根据三角形外角性质求出∠DQA=∠ABC,即可求出答案.
(3)求出CP=AD,∠ACP=∠BAD,根据SAS推出△ABD≌△ACP,求出∠CAP=∠ABD,求出∠AQD=∠CAP+∠QAB=180°-∠CAB,即可求出答案.
(2)根据△BDC≌△APB得出∠CBD=∠BAP,根据三角形外角性质求出∠DQA=∠ABC,即可求出答案.
(3)求出CP=AD,∠ACP=∠BAD,根据SAS推出△ABD≌△ACP,求出∠CAP=∠ABD,求出∠AQD=∠CAP+∠QAB=180°-∠CAB,即可求出答案.
解答:解:(1)在爬行过程中,BD和AP始终相等,
理由是:∵△ABC是等边三角形,
∴∠CAB=∠C=∠ABP=60°,AB=BC,
在△BDC和△APB中,
,
∴△BDC≌△APB(SAS),
∴BD=AP.
(2)蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,
理由:∵△BDC≌△APB,
∴∠CBD=∠BAP,
∴∠DQA=∠DBA+∠BAP=∠DBA+∠CBD=∠ABC=60°,
即蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,始终是60°.
(3)蜗牛爬行过程中的∠DQA大小变化了,
理由是:根据题意得:BP=CD,
∵BC=AC,
∴CP=AD,
∵△ABC是等边三角形,
∴AC=AB,∠CAB=∠ACB=60°,
∵∠ACP+∠ACB=180°,∠DAB+∠CAB=180°,
∴∠ACP=∠BAD,
在△ABD和△ACP中,
,
∴△ABD≌△ACP(SAS),
∴∠CAP=∠ABD,
∴∠AQD=∠ABD+∠BAQ=∠CAP+∠QAB
=180°-∠CAB
=180°-60°
=120°,
即蜗牛爬行过程中的∠DQA大小变化了,等于120°.
理由是:∵△ABC是等边三角形,
∴∠CAB=∠C=∠ABP=60°,AB=BC,
在△BDC和△APB中,
|
∴△BDC≌△APB(SAS),
∴BD=AP.
(2)蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,
理由:∵△BDC≌△APB,
∴∠CBD=∠BAP,
∴∠DQA=∠DBA+∠BAP=∠DBA+∠CBD=∠ABC=60°,
即蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,始终是60°.
(3)蜗牛爬行过程中的∠DQA大小变化了,
理由是:根据题意得:BP=CD,
∵BC=AC,
∴CP=AD,
∵△ABC是等边三角形,
∴AC=AB,∠CAB=∠ACB=60°,
∵∠ACP+∠ACB=180°,∠DAB+∠CAB=180°,
∴∠ACP=∠BAD,
在△ABD和△ACP中,
|
∴△ABD≌△ACP(SAS),
∴∠CAP=∠ABD,
∴∠AQD=∠ABD+∠BAQ=∠CAP+∠QAB
=180°-∠CAB
=180°-60°
=120°,
即蜗牛爬行过程中的∠DQA大小变化了,等于120°.
点评:本题考查了等边三角形的性质,三角形外角性质,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 (1)如图1所示,在等边△ABC中,点D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE,求证:AE∥BC;
(1)如图1所示,在等边△ABC中,点D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE,求证:AE∥BC;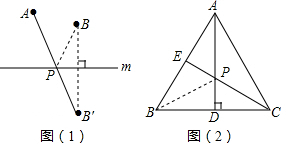

 如图,已知:在等边三角形ABC中,D、E分别在AB和AC上,且AD=CE,BE和CD相交于点P.
如图,已知:在等边三角形ABC中,D、E分别在AB和AC上,且AD=CE,BE和CD相交于点P.