题目内容
10. 抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).
抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).(1)求该抛物线的解析式;
(2)若F为x轴上一点,且FO=OP,求点F的坐标;
(3)若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标.
分析 (1)利用待定系数法即可求得抛物线的解析式;
(2)设F(q,0),利用已知条件FO=OP列出关于q的方程,通过解方程求得q的值,易得F点的坐标;
(3)根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;
解答 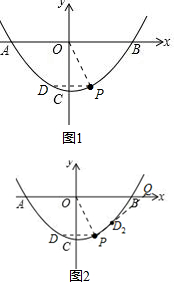 解:(1)将P(1,-3)、B(4,0)代入y=ax2+c,得
解:(1)将P(1,-3)、B(4,0)代入y=ax2+c,得
$\left\{\begin{array}{l}16a+c=0\\ a+c=-3\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{5}}\\{c=-\frac{16}{5}}\end{array}\right.$.
抛物线的解析式为:y=$\frac{1}{5}$x2-$\frac{16}{5}$;
(2)设F(q,0),则12+32=q2,
解得:q=$±\sqrt{10}$,
∴点F的坐标为$({\sqrt{10},0})$,$({-\sqrt{10},0})$;
(3)如图1:当D在P左侧时,
由∠DPO=∠POB得DP∥OB.
D与P关于y轴对称,P(1,-3)得D(-1,-3).
如图2,当D在P右侧时,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,
∴Q(5,0),
则直线PD2为y=$\frac{3}{4}$x-$\frac{15}{4}$,
再联立$\left\{\begin{array}{l}{y=\frac{3}{4}x-\frac{15}{4}}\\{y=\frac{1}{5}{x}^{2}-\frac{16}{5}}\end{array}\right.$ 得:x=1或$\frac{11}{4}$,
∴D2($\frac{11}{4}$,-$\frac{27}{16}$ ).
∴点D的坐标为(-1,-3)或($\frac{11}{4},-\frac{27}{16}$).
点评 本题综合考查抛物线与x轴的交点、待定系数法、二次函数的应用等知识,解题的关键是灵活运用所学知识,学会利用参数构建方程解决问题,所以中考常考题型.

| A. | 最简分数都是真分数 | |
| B. | 分母是7的真分数只有6个 | |
| C. | 假分数比1大 | |
| D. | 分数可分为真分数、假分数和带分数 |
 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则A2017的坐标为( )
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则A2017的坐标为( )| A. | 2015$\sqrt{3}$,2017 | B. | 2016$\sqrt{3}$,2018 | C. | 2017$\sqrt{3}$,2019 | D. | 2017$\sqrt{3}$,2017 |
 抛物线y=x2-2mx+m2-4与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
抛物线y=x2-2mx+m2-4与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
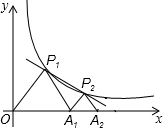 如图,P1、P2(P2在P1的右侧)是y=$\frac{k}{x}$(k>0)在第一象限上的两点,点A1的坐标为(2,0).
如图,P1、P2(P2在P1的右侧)是y=$\frac{k}{x}$(k>0)在第一象限上的两点,点A1的坐标为(2,0). 如图,∠AOB=120°,∠BOD=90°,OC平分∠BOD,求∠AOC的度数.
如图,∠AOB=120°,∠BOD=90°,OC平分∠BOD,求∠AOC的度数.