题目内容
已知:在△ABC中,∠ABC<60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C,D重合),且∠EAC=2∠EBC.

(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB= °,∠AEC= °;
(2)如图2.①求证:AE+AC=BC; ②若∠ECB=30°,且AC=BE,求∠EBC的度数.
(1)54;99;(2)①、见解析;②、20°.
【解析】
试题分析:(1)根据三角形的内角和定理以及等腰三角形的性质进行求解;(2)利用截取法来证明△ACE和△FCE全等,然后通过角度之间的关系来进行求解.
试题解析:(1)54,99;
(2)①证明:在CB上截取CF,使CF=CA,连接EF.(如图)

∵CD平分∠ACB, ∴∠1=∠2.
在△ACE和△FCE中,AC=FC,∠1=∠2, EC=EC,
∴△ACE≌△FCE.
∴∠3=∠4, AE=FE.
∵∠4=∠5+∠6, ∴∠3=∠5+∠6.
∵∠3=2∠6, ∴∠5=∠6.
∴FB=FE. ∴AE=FB. ∴AE+AC= FB+FC= BC.
②【解析】
连接AF.(如图) ∵∠1=∠2=30°,

∴∠ACF=∠1+∠2=60°. ∵AC=FC,
∴△ACF是等边三角形. ∴AF=AC,∠FAC=60°.
∵AC=BE, ∴BE=AF.
在△BFE和△AEF中, BF=AE, FE=EF, BE=AF,
∴△BFE≌△AEF. ∴∠6=∠7.
∵∠7+∠3=60°, ∴∠6+∠3=60°. ∵∠3=2∠6, ∴∠6+2∠6=60°. ∴∠6=20°.
即∠EBC=20°.
考点:三角形全等的证明及性质,角度之间的关系.

 -6x+8=0的解,则△ABC的周长为______
-6x+8=0的解,则△ABC的周长为______ B.
B.
 D.
D.
 ,其中
,其中 .
.
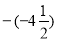 , +3 , 0 ,
, +3 , 0 , 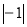 , -
, -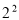 ,
, 

 B.
B. C.
C. D.
D.