题目内容
13.一次远足活动中,一部分人步行,另一部分乘一辆汽车,两部分人同地出发.汽车速度60公里/小时,我们的速度是5公里/小时,步行者比汽车提前2小时出发,当汽车到达目的地后,再回头接步行这部分人.已知出发地到目的地的距离是70公里.问:步行者在出发后经多少时间与回头接他们的汽车相遇?分析 设路人的路程为x+10公里,根据题意找出等量关系:步行者出发两小时后再走x公路的时间=汽车行驶(70+60-x)公里的时间,依此等量关系列出方程求解即可
解答 解:设路人的路程为x+10公里,
由题意得:$\frac{x}{5}$=$\frac{70+60-x}{60}$,
解得:x=10,
$\frac{x+10}{5}$=4小时.
答:步行者在出发后4小时与回头接他们的汽车相遇.
点评 此题考查一元一次方程的实际运用,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列各数:-6,-3.14,π,$\frac{1}{3}$,0,0.212121,其中分数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.如果|a-b|=2,|b-c|=3,|c-d|=4.那么|a-d|的结果有几种不同的值,这些不同值的和为( )
| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
5.函数y=-x+m与y=nx-4的图象的交点坐标为(-1,0),则m、n的值分别为( )
| A. | -1,-4 | B. | 1,4 | C. | -1,4 | D. | 1,-4 |
2. 有理数a、b在数轴上的位置如图所示,则数-a、-b的大小关系为( )
有理数a、b在数轴上的位置如图所示,则数-a、-b的大小关系为( )
 有理数a、b在数轴上的位置如图所示,则数-a、-b的大小关系为( )
有理数a、b在数轴上的位置如图所示,则数-a、-b的大小关系为( )| A. | -b>-a | B. | -b<-a | C. | -b=-a | D. | 不能确定 |
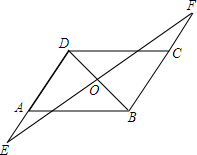 已知:如图,AB=DC,AD=BC,O是BD中点,过O的直线分别与DA,BC的延长线交于E,F,求证:OE=OF.
已知:如图,AB=DC,AD=BC,O是BD中点,过O的直线分别与DA,BC的延长线交于E,F,求证:OE=OF. 如图,AB⊥AC,BE平分∠ABC,CD⊥AC交BE延长线于D,若∠D=25°,求∠ABC的度数.
如图,AB⊥AC,BE平分∠ABC,CD⊥AC交BE延长线于D,若∠D=25°,求∠ABC的度数.