题目内容
设二次函数y=-x2-mx+m+2的图象顶点为A,与x轴两个交点为B、C,则△ABC的面积的最小值是________.
1
分析:设出函数与x轴的交点坐标,利用根与系数的关系求出BC长度的表达式,再求出抛物线的顶点坐标,然后表示出△ABC的面积并化为完全平方式,即可求出△ABC的面积的最小值.
解答:设B(x1,0),C(x2,0),则x1,x2,是方程-x2-mx+m+2=0的两实根,
由根与系数的关系得,x1+x2=-m,x1•x2=-(m+2),
则|BC|=|x2-x1|=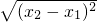 =
= =
= ,
,
又顶点纵坐标为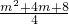 ,
,
故S△ABC=

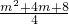 ,
,
由m2+4m+8=(m+2)2+4得,
当m=-2时,△ABC的面积最小,为1.
故答案为:1.
点评:此题考查了二次函数图象与x轴交点间的距离和抛物线的顶点坐标的求法.将面积问题转化为二次函数最值问题是解答的关键.
分析:设出函数与x轴的交点坐标,利用根与系数的关系求出BC长度的表达式,再求出抛物线的顶点坐标,然后表示出△ABC的面积并化为完全平方式,即可求出△ABC的面积的最小值.
解答:设B(x1,0),C(x2,0),则x1,x2,是方程-x2-mx+m+2=0的两实根,
由根与系数的关系得,x1+x2=-m,x1•x2=-(m+2),
则|BC|=|x2-x1|=
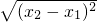 =
= =
= ,
,又顶点纵坐标为
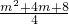 ,
,故S△ABC=


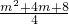 ,
,由m2+4m+8=(m+2)2+4得,
当m=-2时,△ABC的面积最小,为1.
故答案为:1.
点评:此题考查了二次函数图象与x轴交点间的距离和抛物线的顶点坐标的求法.将面积问题转化为二次函数最值问题是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 设二次函数y1=x2-4x+3的图象为C1,二次函数y2=ax2+bx+c(a≠0)的图象与C1关于y轴对称.
设二次函数y1=x2-4x+3的图象为C1,二次函数y2=ax2+bx+c(a≠0)的图象与C1关于y轴对称.