题目内容
 如图,直线l1的关系式为y1=
如图,直线l1的关系式为y1=| 3 |
| 4 |
| 3 |
| 4 |
(1)求直线l2的函数关系式y2;
(2)求△ADC的面积;
(3)根据图象填空,当x
(4)如图(2)过点C作CE⊥x轴于点E,在线段OA上有一点F,将△CEF沿CF折叠,点E恰好与线段CD上的点G重合,求点F的坐标.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得函数关系式;
(2)根据自变量的值,可得C点的纵坐标,根据函数值为零,可得点D的横坐标,根据三角形的面积公式,可得答案;
(3)根据观察图象,l1的图象在上方的部分自变量的取值范围是不等式的解集,可得到答案;
(4)根据翻折的性质,可得EF与FG的关系,根据点到直线的距离公式,可得方程,根据解方程,可得答案.
(2)根据自变量的值,可得C点的纵坐标,根据函数值为零,可得点D的横坐标,根据三角形的面积公式,可得答案;
(3)根据观察图象,l1的图象在上方的部分自变量的取值范围是不等式的解集,可得到答案;
(4)根据翻折的性质,可得EF与FG的关系,根据点到直线的距离公式,可得方程,根据解方程,可得答案.
解答:解:如图:

(1)设直线l2的解析式为y2=kx+b,
由直线l2经过定点A(4,0),B(0,12),得
,解得
.
直线l2的解析式为y2=-3x+12;
(2)C在直线l2上,当x=3时,y=-3×3+12=3.
D在直线l1上,当y=0时,x=-1,即D(-1,0).
S△ADC=
•AD•CE=
×(4+1)×3=7.5;
(3)观察图象,得l1的图象在l2图象上方的部分,即x>3时,y1>y2,
故答案为:x>3;
(4)设F点坐标为(a,0),EF=3-a.
由点到直线l1的距离,得FG=
由△CEF沿CF折叠,得
EF=FG.
3-a=
,
化简,得
a2-21a+27=0
解得a=
,a=9(不符合题意舍去)
点F的坐标是(
,0).

(1)设直线l2的解析式为y2=kx+b,
由直线l2经过定点A(4,0),B(0,12),得
|
|
直线l2的解析式为y2=-3x+12;
(2)C在直线l2上,当x=3时,y=-3×3+12=3.
D在直线l1上,当y=0时,x=-1,即D(-1,0).
S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)观察图象,得l1的图象在l2图象上方的部分,即x>3时,y1>y2,
故答案为:x>3;
(4)设F点坐标为(a,0),EF=3-a.
由点到直线l1的距离,得FG=
|
| ||||
|
由△CEF沿CF折叠,得
EF=FG.
3-a=
|
| ||||
|
化简,得
a2-21a+27=0
解得a=
| 3 |
| 2 |
点F的坐标是(
| 3 |
| 2 |
点评:本题考查了一次函数的综合题,利用了待定系数法求解析式,函数与不等式的关系,图形翻折的性质,点到直线的距离.

练习册系列答案
相关题目
 如图,一人拿着一支厘米小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上12厘米的长度恰好遮住电线杆,已知手臂长约60厘米,则电线杆的高为
如图,一人拿着一支厘米小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上12厘米的长度恰好遮住电线杆,已知手臂长约60厘米,则电线杆的高为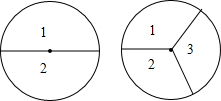 如图,图中的两个转盘分别被均匀地分成2个和3个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
如图,图中的两个转盘分别被均匀地分成2个和3个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )