题目内容
已知:
=
=
=k,试判断直线y=kx+k一定经过哪些象限,并说明理由.
| b+c |
| a |
| a+c |
| b |
| a+b |
| c |
分析:由于a+b+c的符号不能确定,故进行分类讨论,当a+b+c≠0时,可利用等比性质求出k的值,当a+b+c=0时,可将a+b转化为-c,然后求出k,得到其解析式,进而判断出直线y=kx+k一定经过哪些象限.
解答:解:直线y=kx+k一定经过第二、三象限,理由如下:
当a+b+c≠0时,
∵
=
=
=k,
∴k=
=
=2,
此时,y=kx+k=2x+2,经过第一、二、三象限;
当a+b+c=0时,b+c=-a,此时,k=
=
=-1,
此时,y=kx+x=-x-1经过第二、三、四象限.
综上所述,y=kx+k一定经过第二、三象限.
当a+b+c≠0时,
∵
| b+c |
| a |
| a+c |
| b |
| a+b |
| c |
∴k=
| b+c+a+c+a+b |
| a+b+c |
| 2(a+b+c) |
| a+b+c |
此时,y=kx+k=2x+2,经过第一、二、三象限;
当a+b+c=0时,b+c=-a,此时,k=
| b+c |
| a |
| -a |
| a |
此时,y=kx+x=-x-1经过第二、三、四象限.
综上所述,y=kx+k一定经过第二、三象限.
点评:本题考查了一次函数的性质,根据已知条件求出k的值是解题的关键,要熟悉等比性质,并能进行分类讨论.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知:k=
=
=
,则k的值是( )
| c |
| a+b |
| a |
| b+c |
| b |
| c+a |
A、
| ||
| B、-1 | ||
| C、1 | ||
D、
|
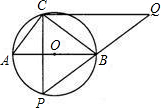 半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在
半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在
 如图,在⊙O中,直径AB的不同侧有点C和点P.已知BC:CA=4:3,点P和点C关于AB所在直线对称,过点C作CP的垂线与PB的延长线交于点Q,且CQ=
如图,在⊙O中,直径AB的不同侧有点C和点P.已知BC:CA=4:3,点P和点C关于AB所在直线对称,过点C作CP的垂线与PB的延长线交于点Q,且CQ=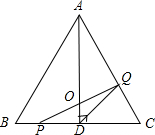 运动,速度为1cm/s,Q沿CA、AB向终点B运动,速度为2cm/s,设它们的运动时间为x(s).
运动,速度为1cm/s,Q沿CA、AB向终点B运动,速度为2cm/s,设它们的运动时间为x(s).