题目内容
 如图,在⊙O中,直径AB的不同侧有点C和点P.已知BC:CA=4:3,点P和点C关于AB所在直线对称,过点C作CP的垂线与PB的延长线交于点Q,且CQ=12
如图,在⊙O中,直径AB的不同侧有点C和点P.已知BC:CA=4:3,点P和点C关于AB所在直线对称,过点C作CP的垂线与PB的延长线交于点Q,且CQ=12| 4 | 5 |
分析:根据题意得CP⊥AB,设垂足为D,由圆周角定理得∠ACB=90°,设BC=4x,那么AC=3x,再根据直角三角形的面积公式可得出CD,PC,再由Rt△ACB∽Rt△PCQ可得出x,由勾股定理求出答案即可.
解答: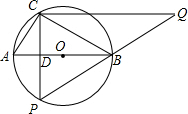 解:∵点P与点C关于AB对称时,CP⊥AB,设垂足为D,
解:∵点P与点C关于AB对称时,CP⊥AB,设垂足为D,
∵AB为⊙O的直径,
∴∠ACB=90°,
BC:CA=4:3,
设BC=4x,那么AC=3x,由勾股定理得:AB=5x
∵
AC•BC=
AB•CD,
∴CD=
x,
∴PC=
x,
在Rt△ACB和Rt△PCQ中,∠ACB=∠PCQ=90°,∠CAB=∠CPQ,
∴Rt△ACB∽Rt△PCQ.
∴
=
,
=
,
解得x=2,
∴直径AB=10,
∴⊙O的半径长为5.
 解:∵点P与点C关于AB对称时,CP⊥AB,设垂足为D,
解:∵点P与点C关于AB对称时,CP⊥AB,设垂足为D,∵AB为⊙O的直径,
∴∠ACB=90°,
BC:CA=4:3,
设BC=4x,那么AC=3x,由勾股定理得:AB=5x
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 12 |
| 5 |
∴PC=
| 24 |
| 5 |
在Rt△ACB和Rt△PCQ中,∠ACB=∠PCQ=90°,∠CAB=∠CPQ,
∴Rt△ACB∽Rt△PCQ.
∴
| AC |
| PC |
| BC |
| CQ |
| 3x | ||
|
| 4x | ||
12
|
解得x=2,
∴直径AB=10,
∴⊙O的半径长为5.
点评:本题是一道有关圆的知识的题目,考查了圆周角定理以及相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
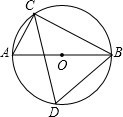 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=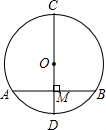 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.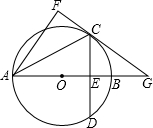 C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )