题目内容
在△ABC中,已知∠A=60°,∠C=75°,AB=10,点D、E、F分别在边AB、BC、CA上,则△DEF周长的最小值
.
考点:轴对称-最短路线问题
专题:计算题
分析:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,如图所示,得到DA平分∠FDE,EB平分∠DEF,FC平分∠EFD,作D关于AB的对称点D′,作D关于AC的对称点D″,则D′、F、E、D″四点共线,△DEF的周长DE+EF+FD=D″E+EF+FD′=D′D″,延长D′D″交BC延长线于点K,则有∠BD′K=60°,∠DEK=90°,∠K=30°,求出D′K=2BD′=10
,DK=BK-
BD=5
-5
,由D″K=EK-ED″=EK-ED,求出D″K的长,根据D′K-D″K求出D′D″的长,即为△DEF周长的最小值.
| 2 |
| 3 |
| 6 |
| 2 |
解答: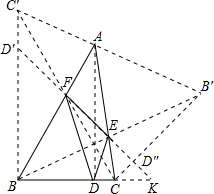 解:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,
解:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,
此时DA平分∠FDE,EB平分∠DEF,FC平分∠EFD,
如图,作D关于AB的对称点D′,作D关于AC的对称点D″,则D′、F、E、D″四点共线,
△DEF的周长DE+EF+FD=D″E+EF+FD′=D′D″,
延长D′D″交BC延长线于点K,则有∠BD′K=60°,∠DEK=90°,∠K=30°,
∵BD′=BD=
AB=5
,
∴D′K=2BD′=10
,DK=BK-
BD=BD′-
AB=5
-5
,
∴D″K=EK-ED″=EK-ED=
DK-
DK=
(5
-5
)-
(5
-5
)=10
-5
,
则D′D″=D′K-D″K=10
-(10
-5
)=5
,即△DEF周长的最小值为5
.
 解:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,
解:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,此时DA平分∠FDE,EB平分∠DEF,FC平分∠EFD,
如图,作D关于AB的对称点D′,作D关于AC的对称点D″,则D′、F、E、D″四点共线,
△DEF的周长DE+EF+FD=D″E+EF+FD′=D′D″,
延长D′D″交BC延长线于点K,则有∠BD′K=60°,∠DEK=90°,∠K=30°,
∵BD′=BD=
| ||
| 2 |
| 2 |
∴D′K=2BD′=10
| 2 |
| 3 |
| ||
| 2 |
| 6 |
| 2 |
∴D″K=EK-ED″=EK-ED=
| ||
| 2 |
| 1 |
| 2 |
| 2 | ||
|
| 6 |
| 2 |
| 1 |
| 2 |
| 6 |
| 2 |
| 2 |
| 6 |
则D′D″=D′K-D″K=10
| 2 |
| 2 |
| 6 |
| 6 |
| 6 |
点评:本题考查了利用轴对称确定最短路线问题,其理论依据是三角形的两边之和大于第三边,作出对称点是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
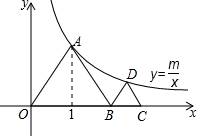 如图,边长为2的等边三角形AOB的顶点在反比例函数y=
如图,边长为2的等边三角形AOB的顶点在反比例函数y=| m |
| x |
A、
| ||||||
B、
| ||||||
C、2
| ||||||
D、2
|
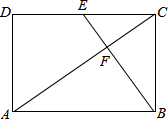 如图,矩形ABCD中,BE⊥AC于F,E恰是CD的中点,请问BF和AF之间存在怎样的数量关系?并请证明.
如图,矩形ABCD中,BE⊥AC于F,E恰是CD的中点,请问BF和AF之间存在怎样的数量关系?并请证明.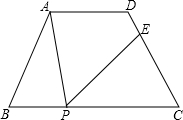 如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长.
如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长. 如图,某校广场有一段25米差个的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.
如图,某校广场有一段25米差个的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.