题目内容
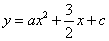
.如图,已知二次函数 的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
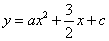 (1)请直接写出二次函数
(1)请直接写出二次函数 的表达式;
的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
 |
解:(1)抛物线表达式: ………2分
………2分
(2)△ABC是直角三角形 ……………………3分
令y=0,则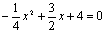 解得,x1=8,x2=-2
解得,x1=8,x2=-2
∴点B的坐标为(-2,0) …………………4分
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20
在Rt△AOC中AC2=AO2+CO2=42+82=80
又∵BC=OB+OC=2+8=10
∴在△ABC中AB2+ AC2=20+80=102=BC2
∴△ABC是直角三角形 …………………6分
(3)坐标分别为(-8,0)、(8-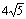 ,0)、(3,0)、(8+
,0)、(3,0)、(8+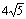 ,0)……………10分
,0)……………10分
(4) 设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,…11分
设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,…11分
 ∴MD∥OA
∴MD∥OA
∴△BMD∽△BAO
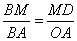 ∴
∴
∵MN∥AC
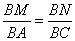 ∴
∴
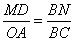 ∴
∴
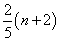
 ∵OA=4,BC=10,BN=n+2
∵OA=4,BC=10,BN=n+2
∴MD=
∵S△AMN= S△ABN- S△BMN
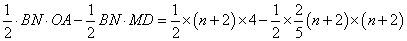 =
=
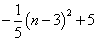 = ……………………13分
= ……………………13分
∴当△AMN面积最大时,N点坐标为(3,0)

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 BOD=88°,则∠BCD的度数是( )
BOD=88°,则∠BCD的度数是( ) 
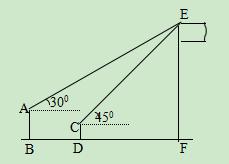
 ,
, )
)
 .
. 数字3的小球的概率是 ;
数字3的小球的概率是 ; 的解是( )
的解是( )
 B.
B.  C.
C. D.
D.

 B.
B. C.
C. D.
D.