题目内容
8.(1)解方程:(x-1)2=9(2)计算:${(-\sqrt{3})^2}-\sqrt{{{(-4)}^2}}-\root{3}{-8}-|{1-\sqrt{2}}|$
(3)计算:$\frac{{\sqrt{27}+\sqrt{48}}}{{\sqrt{3}}}$
(4)计算:$(\sqrt{7}+\sqrt{3})(\sqrt{7}-\sqrt{3})-{(2+\sqrt{5})^2}$.
分析 (1)方程利用平方根定义开方即可求出解;
(2)原式利用平方根定义,二次根式性质,立方根定义,以及绝对值的代数意义计算即可得到结果;
(3)原式利用二次根式的除法法则计算即可得到结果;
(4)原式利用平方差公式及完全平方公式计算即可得到结果.
解答 解:(1)开方得:x-1=3或x-1=-3,
解得:x1=4,x2=-2;
(2)原式=3-4+2-$\sqrt{2}$+1=2-$\sqrt{2}$;
(3)原式=$\sqrt{\frac{27}{3}}$+$\sqrt{\frac{48}{3}}$=3+4=7;
(4)原式=7-3-4-4$\sqrt{5}$-5=-4$\sqrt{5}$-5.
点评 此题考查了实数的运算,以及解一元二次方程-直接开平方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.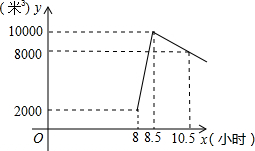 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了8000米3的天然气;
(2)当x≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式y=-1000x+18500;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气9600米3;
(4)这第20辆车在当天9:00之前不能加完气;
其中说法正确的有( )
 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.(1)8:00~8:30,燃气公司向储气罐注入了8000米3的天然气;
(2)当x≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式y=-1000x+18500;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气9600米3;
(4)这第20辆车在当天9:00之前不能加完气;
其中说法正确的有( )
| A. | (1)(2) | B. | (2)(3) | C. | (1)(2)(3) | D. | (1)(2)(3)(4) |
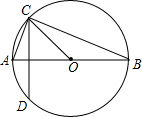 如图,AB是⊙O的直径,弦CD垂直AB,已知AC=1,BC=2$\sqrt{2}$,那么sin∠ACD的值是$\frac{1}{3}$.
如图,AB是⊙O的直径,弦CD垂直AB,已知AC=1,BC=2$\sqrt{2}$,那么sin∠ACD的值是$\frac{1}{3}$.