题目内容
15.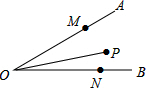 如图,∠AOB=α,P在∠AOB内,OP=2,M和N分别为OA,OB上一动点,当△PMN的周长为最小值2时,α=30°.
如图,∠AOB=α,P在∠AOB内,OP=2,M和N分别为OA,OB上一动点,当△PMN的周长为最小值2时,α=30°.
分析 作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等边三角形,据此即可求解.
解答 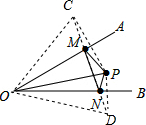 解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.
解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.
∵PC关于OA对称,
∴∠COP=2∠AOP,OC=OP,
同理,∠DOP=2∠BOP,OP=OD,
∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB,OC=OD=OP=2.
∵CD=2,
∴△COD是等边三角形.
∴∠COD=2∠AOB=60°,
∴∠AOB=30°,
∴α=30°,
故答案为30°.
点评 本题考查了对称的性质,等腰直角三角形的判定和性质以及勾股定理的运用,解题的关键是正确作出图形,理解△PMN周长最小的条件是解题的关键.

练习册系列答案
相关题目
6.下列各组数中互为相反数的是( )
| A. | $\frac{1}{5}$与$\sqrt{(-5)^{2}}$ | B. | -3与$\frac{1}{3}$ | C. | -3与$\root{3}{-27}$ | D. | -(-2)与-|-2| |
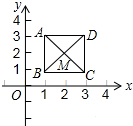 如图,已知正方形ABCD,顶点A(1,3)、B(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).
如图,已知正方形ABCD,顶点A(1,3)、B(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).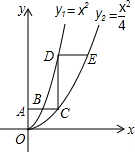 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B,C两点,过点C作y轴的平行交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=2.
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B,C两点,过点C作y轴的平行交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=2. 如图,在一块边长为2a m的正方形土地上,挖一个正方形的池塘,池塘四周的堤坝占地面积是4b2 m2,求当a=3.5.b=1.5时池塘的面积.
如图,在一块边长为2a m的正方形土地上,挖一个正方形的池塘,池塘四周的堤坝占地面积是4b2 m2,求当a=3.5.b=1.5时池塘的面积.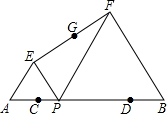 如图:已知AB=16,点C、D在线段AB上且AC=DB=3; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( )
如图:已知AB=16,点C、D在线段AB上且AC=DB=3; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( )