题目内容
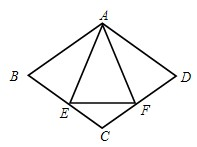
 如图,菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EG⊥CD于点G,则∠FGC=
如图,菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EG⊥CD于点G,则∠FGC=分析:延长GF交AB的延长线于点P.根据已知可得∠EBF,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EGF的度数,从而不难求得∠FGC的度数.
解答:解:延长GF,交AB的延长线于点P.
∵F为BC的中点,
∴BF=CF,
∵四边形ABCD为菱形,
∴AB∥DC,
∴∠PBF=∠GCF,∠BFP=∠CFG,
在△BPF与△CGF中,
,
∴△BPF≌△CGF,
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEG=90°,
∴EF=
PG,
∵GF=
PG,
∴EF=GF,
∴∠FEG=∠EGF,
∵∠BEG=∠EGC=90°,
∴∠BEG-∠FEG=∠EGC-∠EGF,即∠BEF=∠FGC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=
(180°-70°)=55°,
∴∠FGC=55°.
故答案为55°.

∵F为BC的中点,
∴BF=CF,
∵四边形ABCD为菱形,
∴AB∥DC,
∴∠PBF=∠GCF,∠BFP=∠CFG,
在△BPF与△CGF中,
|
∴△BPF≌△CGF,
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEG=90°,
∴EF=
| 1 |
| 2 |
∵GF=
| 1 |
| 2 |
∴EF=GF,
∴∠FEG=∠EGF,
∵∠BEG=∠EGC=90°,
∴∠BEG-∠FEG=∠EGC-∠EGF,即∠BEF=∠FGC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=
| 1 |
| 2 |
∴∠FGC=55°.
故答案为55°.
点评:本题主要考查了菱形的性质和全等三角形的判定等知识点,灵活应用菱形的性质是解决问题的关键,此题难度一般,作出辅助线也很关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
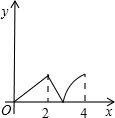
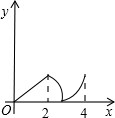
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )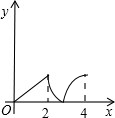
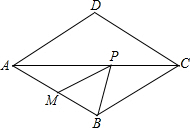 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,