题目内容
如图,直线y=x+1与y轴交于A点,与反比例函数
 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
 .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数
 (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.


【考点】反比例函数综合题.
【专题】计算题.
【分析】(1)对于直线y=x+1,令x=0求出y的值,确定出A坐标,得到OA的长,根据tan∠AHO的值,利用锐角三角函数定义求出OH的长,根据MH垂直于x轴,得到M横坐标与A横坐标相同,再由M在直线y=x+1上,确定出M坐标,代入反比例解析式求出k的值即可;
(2)将N坐标代入反比例解析式求出a的值,确定出N坐标,过N作N关于y轴的对称点N1,连接MN1,交y轴于P(如图),此时PM+PN最小,由N与N1关于y轴的对称,根据N坐标求出N1坐标,设直线MN1的解析式为y=kx+b,把M,N1的坐标代入求出k与b的值,确定出直线MN1的解析式,令x=0求出y的值,即可确定出P坐标.
【解答】解:(1)由y=x+1可得A(0,1),即OA=1,
∵tan∠AHO=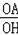
 =
=
 ,
,
∴OH=2,
∵MH⊥x轴,
∴点M的横坐标为2,
∵点M在直线y=x+1上,
∴点M的纵坐标为3,即M(2,3),
∵点M在y=
 上,
上,
∴k=2×3=6;
(2)∵点N(1,a)在反比例函数y=
 的图象上,
的图象上,
∴a=6,即点N的坐标为(1,6),
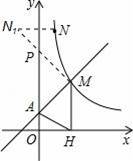
过N作N关于y轴的对称点N1,连接MN1,交y轴于P(如图),
此时PM+PN最小,
∵N与N1关于y轴的对称,N点坐标为(1,6),
∴N1的坐标为(﹣1,6),
设直线MN1的解析式为y=kx+b,
把M,N1的坐标得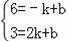
 ,
,
解得: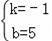
 ,
,
∴直线MN1的解析式为y=﹣x+5,
令x=0,得y=5,
∴P点坐标为(0,5).

【点评】此题属于反比例函数综合题,涉及的知识有:锐角三角函数定义,待定系数法求一次函数解析式,对称的性质,以及一次函数与坐标轴的交点,熟练掌握待定系数法是解本题的关键.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
 与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )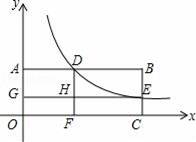

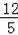
 B.
B.
 +1 C.
+1 C.
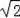

 ,求证:△ABC是“好玩三角形”.
,求证:△ABC是“好玩三角形”.

 的图象经过点(1,2),则它的图象也一定经过的点是( )
的图象经过点(1,2),则它的图象也一定经过的点是( ) 


 点
点 为双曲线
为双曲线 上的一点,且
上的一点,且 轴于点
轴于点 ,
, 轴于点
轴于点 ,
, 分别交双曲线
分别交双曲线 于
于 两点,则
两点,则 的面积是 。
的面积是 。