题目内容
5.(1)计算:$\sqrt{12}$-3tan30°-($\frac{1}{2}$)-2;(2)解不等式组:$\left\{\begin{array}{l}{x+1≥\frac{x}{2}}\\{2x+6>3x+2}\end{array}\right.$.
分析 (1)利用算术平方根以及特殊角的三角函数值和负整数指数幂的性质化简各数求出即可;
(2)分别解不等式进而得出公共解集即可.
解答 解:(1)原式=2$\sqrt{3}$-3×$\frac{\sqrt{3}}{3}$-$\frac{1}{(\frac{1}{2})^{2}}$
=2$\sqrt{3}$-$\sqrt{3}$-4
=$\sqrt{3}$-4;
(2)$\left\{\begin{array}{l}{x+1≥\frac{x}{2}①}\\{2x+6>3x+2②}\end{array}\right.$,
解①得:x≥-2,
解②得:x<4,
故不等式组的解集为:-2≤x<4.
点评 此题主要考查了实数运算以及不等式组的解法,正确掌握相关性质化简各数是解题关键.

练习册系列答案
相关题目
15.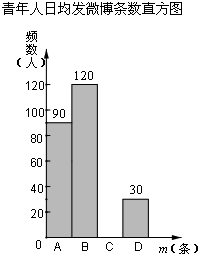 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
青年人日均发微博条数统计表
请你根据以上信息解答下列问题:
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某大城市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微博条数”不少于10条的大约有多少万人.
 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | a |
| C级(10≤m<15) | b | 0.2 |
| D级(15≤m<20) | 30 | 0.1 |
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某大城市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微博条数”不少于10条的大约有多少万人.
16.若关于x的不等式组$\left\{\begin{array}{l}{x>3}\\{x<a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤3 | B. | a≥3 | C. | a<3 | D. | a>3 |
13.下列标志中不是中心对称图形的是( )
| A. |  中国移动 | B. |  中国银行 | C. |  中国人民银行 | D. |  方正集团 |
10.设抛物线y=x2-4x+k的顶点在直线y=x上,则k的值为( )
| A. | -6 | B. | -4 | C. | 4 | D. | 6 |
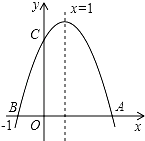 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标是(-1,0),对称轴为直线x=1,下面的四个结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标是(-1,0),对称轴为直线x=1,下面的四个结论: 如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2.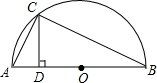 如图所示,AB是半圆O的直径,CD⊥AB,AC=5cm,BC=12cm,求CD的长.
如图所示,AB是半圆O的直径,CD⊥AB,AC=5cm,BC=12cm,求CD的长.