题目内容
15.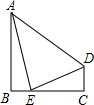 如图,四边形ABCD中,∠ABE=90°,AB∥CD,AB=BC=6,点E为BC边上一点,且∠EAD=45°,ED=5,则△ADE的面积为15.
如图,四边形ABCD中,∠ABE=90°,AB∥CD,AB=BC=6,点E为BC边上一点,且∠EAD=45°,ED=5,则△ADE的面积为15.
分析 过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,先证得△AGB≌△ADF得出AG=AD,∠EAD=∠GAE=45°,然后再证得△ADE≌△AGE,得出EG=ED=5,最后根据全等三角形的面积相等即可求得;
解答  解:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,
解:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,
在△AGB与△ADF中,
$\left\{\begin{array}{l}{AB=AF}\\{∠ABG=∠AFD=90°}\\{BG=DF}\end{array}\right.$,
∴△AGB≌△ADF(SAS),
∴AG=AD,∠GAB=∠DAF,
∴∠GAD=90°
∵∠EAD=45°,
∴∠GAE=45°,
在△ADE与△AGE中,
$\left\{\begin{array}{l}{AG=AD}\\{∠GAE=∠DAE=45°}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AGE(SAS),
∴EG=ED=5,
∴S△ADE=S△AGE=$\frac{1}{2}$EG•AB=$\frac{1}{2}$×5×6=15,
故答案为15.
点评 本题考查了三角形全等的判定和性质,正方形的性质,作出辅助线是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.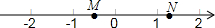 如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
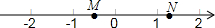 如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-1<n-1 | B. | -m<-n | C. | |m|-|n|>0 | D. | m+n<0 |
10.在平行四边形ABCD中,∠A+∠C=240°,则∠B的度数是( )
| A. | 120° | B. | 80° | C. | 100° | D. | 60° |
4.某商场试销一种成本为80元的衬衫,规定试销期间,利润不低于成本的20%,且获利不得高于50%.经试销发现,销售量y(件)与销售单价x(元)有如下对应关系:
试求销售量y(件)与销售单价x(元)之间的函数关系式.
| 售价x(元/件) | 100 | 105 | 110 | 115 | 120 |
| 销量y(件) | 60 | 50 | 40 | 30 | 20 |
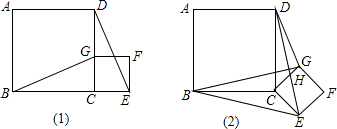
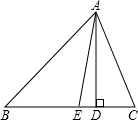 已知:如图,△ABC中,AD是高,AE平分∠BAC,∠B=50°,∠C=80°.求∠DAE的度数.
已知:如图,△ABC中,AD是高,AE平分∠BAC,∠B=50°,∠C=80°.求∠DAE的度数.