题目内容
将一张三角形纸片△ABC沿着DE折叠.
(1)如图①,使点A落在AC边上点A′的位置,试探究∠A与∠1之间的数量关系,并证明你的结论;
(2)如图②,使点A落在四边形BCDE的内部点A′的位置,试探究∠A与∠1+∠2之间的数量关系,并证明你的结论;
(3)如图③,使点A落在四边形BCDE的外部点A′的位置,试直接写出∠A与∠1、∠2之间的数量关系(不必证明).
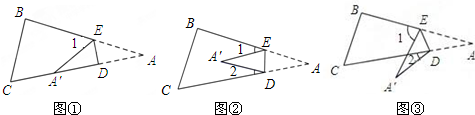
(1)如图①,使点A落在AC边上点A′的位置,试探究∠A与∠1之间的数量关系,并证明你的结论;
(2)如图②,使点A落在四边形BCDE的内部点A′的位置,试探究∠A与∠1+∠2之间的数量关系,并证明你的结论;
(3)如图③,使点A落在四边形BCDE的外部点A′的位置,试直接写出∠A与∠1、∠2之间的数量关系(不必证明).

考点:三角形内角和定理,三角形的外角性质
专题:探究型
分析:(1)运用折叠原理及三角形的外角性质即可解决问题.
(2)运用折叠原理及四边形的内角和定理即可解决问题
(3)运用三角形的外角性质即可解决问题.
(2)运用折叠原理及四边形的内角和定理即可解决问题
(3)运用三角形的外角性质即可解决问题.
解答:解:(1)如图1,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,∴∠1=2∠A.
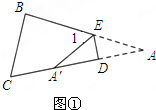
(2)如图2,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′EA+∠2+∠A′DA=360°,
∠A+∠A′+∠A′EA+∠A′DA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得∠A=∠A′,
∴2∠A=∠1+∠2.
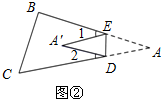
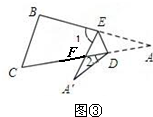
(3)如图3,2∠A=∠1-∠2.
∵∠1=∠EFA+∠A,∠EFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A++∠2,
∴2∠A=∠1-∠2.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,∴∠1=2∠A.

(2)如图2,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′EA+∠2+∠A′DA=360°,
∠A+∠A′+∠A′EA+∠A′DA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得∠A=∠A′,
∴2∠A=∠1+∠2.

(3)如图3,2∠A=∠1-∠2.
∵∠1=∠EFA+∠A,∠EFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A++∠2,
∴2∠A=∠1-∠2.

点评:考查了三角形的内角和定理及外角性质;解题的关键是结合图形灵活运用有关定理来解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、根据加法交换律有4-5-1=-5+1+4 |
| B、5-6可以看成是5加(-6) |
| C、(+7)-(-4)+(-3)=7-4-3 |
| D、根据加法结合律有24-4-3=24-(4-3) |
 如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE的角度为( )
如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE的角度为( )| A、25° | B、35° |
| C、45° | D、55° |
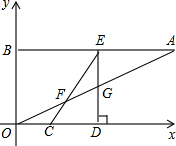 如图,在平面直角坐标系xOy中,点A、B的坐标分别为(16,8)、(0,8),线段CD在x轴上,CD=6,点C从原点出发沿x轴正方向以每秒2个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
如图,在平面直角坐标系xOy中,点A、B的坐标分别为(16,8)、(0,8),线段CD在x轴上,CD=6,点C从原点出发沿x轴正方向以每秒2个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.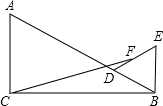 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F为DE中点,则CF的最小值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F为DE中点,则CF的最小值为 如图,在△ABC中,点D在BC上,BD=AD=AC,∠BAC=60°,求∠B的度数.
如图,在△ABC中,点D在BC上,BD=AD=AC,∠BAC=60°,求∠B的度数.
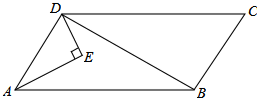 边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.
边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.