题目内容
如图，点P是⊙O直径AB的延长线上一点，PC切⊙O于点C，已知OB=3，PB=2．则PC等于
- A.2
- B.3
- C.4
- D.5
C
分析：根据题意可得出PC2=PB•PA，再由OB=3，PB=2，则PA=8，代入可求出PC．
解答：∵PC、PB分别为⊙O的切线和割线，
∴PC2=PB•PA，
∵OB=3，PB=2，
∴PA=8，
∴PC2=PB•PA=2×8=16，
∴PC=4．
故选C．
点评：本题考查了切割线定理，熟记切割线定理的公式PC2=PB•PA．
分析：根据题意可得出PC2=PB•PA，再由OB=3，PB=2，则PA=8，代入可求出PC．
解答：∵PC、PB分别为⊙O的切线和割线，
∴PC2=PB•PA，
∵OB=3，PB=2，
∴PA=8，
∴PC2=PB•PA=2×8=16，
∴PC=4．
故选C．
点评：本题考查了切割线定理，熟记切割线定理的公式PC2=PB•PA．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
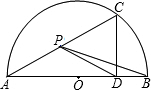
6、如图，点P是⊙O直径AB的延长线上一点，PC切⊙O于点C，已知OB=3，PB=2．则PC等于（ ）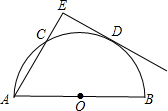
如图，点C是直径为AB的半圆O上一点，D为
如图，点D是⊙O直径CA的延长线上一点，点B在⊙O上，且AB=AD=AO．
于点F，且CF＝9，cos∠BFA＝
，求EF的长．