题目内容
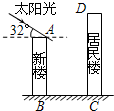某居民小区有一朝向为正南方向的居民楼（如图 ），该居民楼的一楼是高6米的小区超市，超市以上是居民住房．在该楼的前面15米处要盖一栋高20米的新楼．当冬季正午的阳光与水平线的夹角为32°时．（1）问超市以上的居民住房采光是否有影响，为什么？
（2）若要使超市采光不受影响，两楼应相距多少米？
（结果保留整数，参考数据：sin32°≈
| 53 |
| 100 |
| 106 |
| 125 |
| 5 |
| 8 |
分析：（1）利用三角函数算出阳光可能照到居民楼的什么高度，和6米进行比较．
（2）超市不受影响，说明32°的阳光应照射到楼的底部，根据新楼的高度和32°的正切值即可计算．
（2）超市不受影响，说明32°的阳光应照射到楼的底部，根据新楼的高度和32°的正切值即可计算．
解答：
解：（1）如图，设CE=x米，则AF=（20-x）米，tan32°=
，
即20-x=15•tan32°，x≈11，
∵11＞6，
∴居民住房的采光有影响．
（2）如图：
tan32°=
，BC=20÷
=32（米）．
故两楼应相距32米．
解：（1）如图，设CE=x米，则AF=（20-x）米，tan32°=| AF |
| EF |
即20-x=15•tan32°，x≈11，
∵11＞6，
∴居民住房的采光有影响．
（2）如图：tan32°=
| AB |
| BC |
| 5 |
| 8 |
故两楼应相距32米．
点评：本题考查锐角三角函数的应用．需注意直角三角形的构造是常用的辅助线方法．
练习册系列答案
相关题目
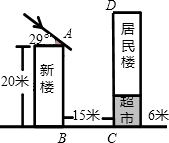夹角为29°．（参考数据：sin29°≈0.48；cos29°≈0.87；tan29°≈0.55）
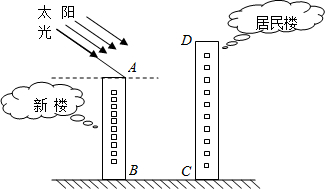居民住房．在该楼的前面15米处要盖一栋高20米的新楼．当冬季正午的阳光与水平线的夹角为32°时．
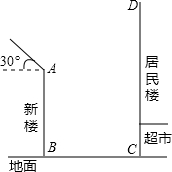（2013•吴江市模拟）冬至是一年中太阳光照射最少的日子，如果此时楼房最低层能采到阳光，一年四季整座楼均能受到阳光照射，所以冬至是选房买房时确定阳光照射的最好时机．吴江某居民小区有一
某居民小区有一朝向为正南的居民楼（如图），该居民楼的一楼是高为6米的小区超市，超市以上是居民住房．在该楼的前面15米处要盖一栋高20米的新楼．当冬季正午的阳光与水平线的夹角是30°时．