题目内容
 (2013•吴江市模拟)冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一
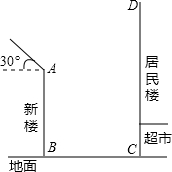
(2013•吴江市模拟)冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高为5米的小区超市,超市以上是居民住房,现计划在该楼前面24米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为30°.(参考数据在
| 2 |
| 3 |
(1)中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
(2)若新建的大楼高18米,则中午时,超市以上的居民住房采光是否受影响,为什么?
分析:(1)连接AC,在Rt△ABC中,利用锐角三角函数表示出线段AB的长,然后保留整数即可求得楼高的范围.
(2)首先过点E作BC平行线角AB与点F.在Rt△AFG中,利用正切函数求得GF的长,即为使得超市采光不受影响,两楼应至少相距的米数.
(2)首先过点E作BC平行线角AB与点F.在Rt△AFG中,利用正切函数求得GF的长,即为使得超市采光不受影响,两楼应至少相距的米数.
解答: 解:(1)连接AC,在Rt△ABC中,
解:(1)连接AC,在Rt△ABC中,
∵tan30°=
∴AB=24×
=8
=8×1.732=13.856
当楼高AB超过13.856时,光线照到C点的上方,超市采光受影响,又结果需要保留整数,所以楼高不超过13米;
(2)设居民楼底与超市顶端交界点为E, 过点E作BC平行线角AB与点F,设过新楼顶的光线交直线EF与点G,则AF=18-5=13,
过点E作BC平行线角AB与点F,设过新楼顶的光线交直线EF与点G,则AF=18-5=13,
在Rt△AFG中,FG=
=
=22.517,
∵FG<FE=24
∴超市以上的居民住房采光不受影响.
 解:(1)连接AC,在Rt△ABC中,
解:(1)连接AC,在Rt△ABC中,∵tan30°=
| AB |
| 24 |
∴AB=24×
| ||
| 3 |
| 3 |
当楼高AB超过13.856时,光线照到C点的上方,超市采光受影响,又结果需要保留整数,所以楼高不超过13米;
(2)设居民楼底与超市顶端交界点为E,
 过点E作BC平行线角AB与点F,设过新楼顶的光线交直线EF与点G,则AF=18-5=13,
过点E作BC平行线角AB与点F,设过新楼顶的光线交直线EF与点G,则AF=18-5=13,在Rt△AFG中,FG=
| 13 |
| tan30° |
| 39 | ||
|
∵FG<FE=24
∴超市以上的居民住房采光不受影响.
点评:此题考查了三角函数的基本概念,主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
 (2013•吴江市模拟)如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是( )
(2013•吴江市模拟)如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是( ) (2013•吴江市模拟)如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AD:DB=4:5,AC=9.
(2013•吴江市模拟)如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AD:DB=4:5,AC=9.