题目内容
 如图,点P(m,n)为抛物线y=-
如图,点P(m,n)为抛物线y=-| 1 |
| 2 |
考点:二次函数综合题
专题:
分析:由圆心P在抛物线y=-
x2-x+1上运动,点P的坐标为(m,n),可得n=-
m2-m+1,又由⊙P半径为1,⊙P与x轴相交,可得|-
m2-m+1|<1,继而可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵圆心P在抛物线y=-
x2-x+1上运动,点P的坐标为(m,n),
∴n=-
m2-m+1,
∵⊙P半径为1,⊙P与x轴相交,
∴|n|<1,
∴|-
m2-m+1|<1,
∴-1<-
m2-m+1<1,
解-
m2-m+1<1,得:m>0或m<-2
解-
m2-m+1>-1,得:-
-1<m<
-1,
∴点P的横坐标m的取值范围是:-
-1<m<-2或0<m<
-1.
故答案为:-
-1<m<-2或0<m<
-1.
| 1 |
| 2 |
∴n=-
| 1 |
| 2 |
∵⊙P半径为1,⊙P与x轴相交,
∴|n|<1,
∴|-
| 1 |
| 2 |
∴-1<-
| 1 |
| 2 |
解-
| 1 |
| 2 |
解-
| 1 |
| 2 |
| 5 |
| 5 |
∴点P的横坐标m的取值范围是:-
| 5 |
| 5 |
故答案为:-
| 5 |
| 5 |
点评:此题考查了二次函数上点的性质、直线与圆的位置关系以及不等式的求解方法.此题难度较大,注意掌握方程思想与数形结合思想的应用

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
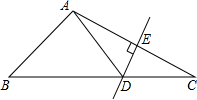 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为( )cm.
如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为( )cm.| A、13 | B、19 | C、10 | D、16 |
 如图,图中共有( )对同位角.
如图,图中共有( )对同位角.| A、2 | B、4 | C、6 | D、8 |
 如图,△ABC中,∠A=35°,∠C=60°,BD平分∠ABC,DE∥BC交AB于E,则∠BDE=
如图,△ABC中,∠A=35°,∠C=60°,BD平分∠ABC,DE∥BC交AB于E,则∠BDE= 如图,∠2=∠3,∠1=62°24′,则∠4=
如图,∠2=∠3,∠1=62°24′,则∠4=