题目内容
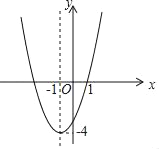
【题目】已知二次函数的图象如图所示.
(1)求这个二次函数的表达式;
(2)将该二次函数图象向上平移 个单位长度后恰好过点(﹣2,0);
(3)观察图象,当﹣2<x<1时,y的取值范围为 .
【答案】(1)y=(x+1)2﹣4;(2)3;(3)﹣4≤y<0.
【解析】
先利用待定系数法求出函数解析式,再利用平移变换求出平移了几个单位长度,最后观察图像写出y的取值范围.
(1)设y=a(x+h)2﹣k.
∵图象经过顶点(﹣1,﹣4)和点(1,0),
∴y=a(x+1)2﹣4.
将(1,0)代入可得a=1,
∴y=(x+1)2﹣4.
(2)设向上平移n个单位,得
y=(x+1)2﹣4+n,
将(﹣2,0)代入,得
1﹣4+n=0,
解得n=3,
故答案为:3.
(3)由图象,得
当﹣2<x<1时,图象位于x轴的下方,图象的顶点坐标是(﹣1,﹣4),
∴﹣4≤y<0,
故答案为:﹣4≤y<0.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目