题目内容
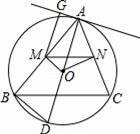
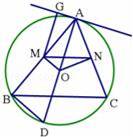
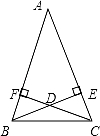
已知:如图,△ABC是⊙O内接三角形,OM⊥AB于点M,ON⊥AC于点N,连接MN,
(1)求证:MN=
 BC;
BC;
(2)过点A作⊙O的直径AD,连接BD,AG为过点A的圆切线,过点M作MG⊥AG,垂足为G,若cos∠BAD=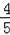
 ,BD=20,求AG的长.
,BD=20,求AG的长.

【考点】切线的性质;勾股定理;三角形中位线定理;垂径定理.
【分析】(1)由垂径定理和三角形的中位线的性质得到结论.
(2)由AD是⊙O的直径,得到∠ABD=90°,解直角三角形得到AD,AB的长度,再由锐角三角函数解出结果.
【解答】(1)证明:∵OM⊥AB于点M,ON⊥AC于点N,
∴点M、N分别是AB、AC的中点,MN是三角形ABC的中位线,
∴MN=
 BC;
BC;
(2)解:∵AD是⊙O的直径,
∴∠ABD=90°,
∵cos∠BAD=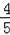
 ,BD=20,
,BD=20,
∴在直角三角形ABD中,可设AD=5k,AB=4K,
根据勾股定理得:(5k)2﹣(4k)2202,
∴k=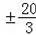
 (﹣
(﹣
 舍去),
舍去),
∴AD=
 ,AB=
,AB=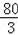
 ,
,
∵AG是⊙O的切线,
∴OA⊥AG,
又∵MG⊥AG,
∴∠GAD=90°=∠MGA,
∴AD∥MG
∴∠AMG=∠BAD
∴sin∠AMG=sin∠BAD=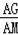
 =
=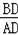
 =
=
 ,
,
∴AG=
 AM=
AM=
 ×
×
 AB=8,
AB=8,
∴AG=8.

【点评】本题考查了三角形的中位线定理,切线的性质,垂径定理,勾股定理,锐角三角函数,掌握垂径定理是解题的关键.

练习册系列答案
相关题目




 .
.