题目内容
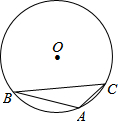 如图,⊙O是△ABC的外接圆,∠BAC=120°,若⊙O的半径OC为2,则弦BC的长为( )
如图,⊙O是△ABC的外接圆,∠BAC=120°,若⊙O的半径OC为2,则弦BC的长为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:在⊙O上找一点E,连接BE,CE,OB,OC,过点O作OD⊥BC于点D,根据圆内接四边形的性质求出∠E的度数,由圆周角定理得出∠BOC的度数,根据垂径定理得出BC=2BD,由直角三角形的性质求出BD的长,进而可得出结论.
解答:
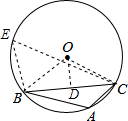 解:在⊙O上找一点E,连接BE,CE,OB,OC,过点O作OD⊥BC于点D,
解:在⊙O上找一点E,连接BE,CE,OB,OC,过点O作OD⊥BC于点D,
∵四边形ABEC是圆内接四边形,∠BAC=120°,
∴∠E=60°,
∴∠BOC=120°,
又∵OD⊥BC,
∴∠BOD=60°,BC=2BD,
∴BD=sin60°×OB=
×2=
,
∴BC=2BD=2
.
故选D.
 解:在⊙O上找一点E,连接BE,CE,OB,OC,过点O作OD⊥BC于点D,
解:在⊙O上找一点E,连接BE,CE,OB,OC,过点O作OD⊥BC于点D,∵四边形ABEC是圆内接四边形,∠BAC=120°,
∴∠E=60°,
∴∠BOC=120°,
又∵OD⊥BC,
∴∠BOD=60°,BC=2BD,
∴BD=sin60°×OB=
| ||
| 2 |
| 3 |
∴BC=2BD=2
| 3 |
故选D.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
相关题目
|a-
|+(b+1)2=0,则ab的值是( )
| 1 |
| 2 |
A、-
| ||
B、±
| ||
C、
| ||
D、
|
如图,把一些相同的菱形,按如图的方式排列,就构成一些大小不同的菱形,其中第一个图形中有3个菱形,第二个图形中有7个菱形,第三个图形中11个菱形,….则第n(n≥1)个图形中有菱形的个数为( )

| A、2n+3 | B、4n+3 |
| C、4n-1 | D、2n+2 |
 如图,点A点B在双曲线y=
如图,点A点B在双曲线y=