Question

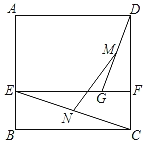
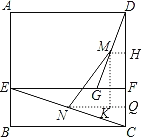
【题目】如图，已知正方形ABCD的边长为4，E，F分别为AB，CD边上的点，且EF∥BC，G为EF上一点，且GF=1，M，N分别为GD，EC的中点，则MN=_____．

Answer 1

【答案】

【解析】

作MH⊥CD于H，NQ⊥CD于Q，MK⊥NQ于K，如图，先证明四边形BCFE为矩形得到EF=BC=4，再根据平行线分线段成比例定理得到，则MH=，DH=DF，同理可得NQ=2，CQ=CF，则HQ=CD=2，易得四边形MKQH为矩形，则KQ=KH=，MK=HQ=2，然后在Rt△MNK中利用勾股定理计算MN的长．

解：作MH⊥CD于H，NQ⊥CD于Q，MK⊥NQ于K，如图，

∵四边形ABCD为正方形，

∴∠BCD=90°，CB=CD=4，

∵EF∥BC，

∴EF⊥CD，

∴四边形BCFE为矩形，

∴EF=BC=4，

∴MH∥EF，NQ∥EF，

∵MH∥GF，

∵，M点为DG的中点，

∴MH=GF=，DH=DF，

同理可得NQ=EF=2，CQ=CF，

∴HQ=(DF+CF)=CD=2，

易得四边形MKQH为矩形，

∴KQ=KH=，MK=HQ=2，

∴NK=NQ﹣KQ=2﹣=，

在Rt△MNK中，MN=．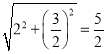

故答案为：．