ĖâÄŋÄÚČÝ
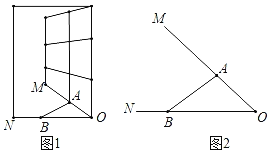
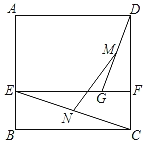
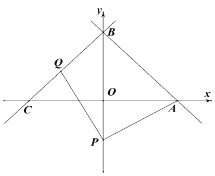
ĄūĖâÄŋĄŋČįÍžĢŽŌŅÖŠÔÚÆ―ÃæÖą―ĮŨøąęÏĩxOyÖÐĢŽÅŨÎïÏßyĢ―ax2+bx+4ūđýĩãAĢĻĐ3ĢŽ0ĢĐšÍĩãBĢĻ3ĢŽ2ĢĐĢŽÓëyÖáÏā―ŧÓÚĩãCĢŪ
ĢĻ1ĢĐĮóÕâĖõÅŨÎïÏßĩÄąíīïĘ―Ģŧ
ĢĻ2ĢĐĩãPĘĮÅŨÎïÏßÔÚĩÚŌŧÏóÏÞÄÚŌŧĩãĢŽÁŠ―áAPĢŽČįđûĩãCđØÓÚÖąÏßAPĩÄķÔģÆĩãDĮĄšÃÂäÔÚxÖáÉÏĢŽĮóÖąÏßAPĩÄ―ØūāĢŧ
ĢĻ3ĢĐÔÚĢĻ2ĢĐÐĄĖâĩÄĖõžþÏÂĢŽČįđûĩãEĘĮyÖáÕý°ëÖáÉÏŌŧĩãĢŽĩãFĘĮÖąÏßAPÉÏŌŧĩãĢŪĩąĄũEAOÓëĄũEAFČŦĩČĘąĢŽĮóĩãEĩÄŨÝŨøąęĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ![]() ĢŧĢĻ2ĢĐ
ĢŧĢĻ2ĢĐ![]() ĢŧĢĻ3ĢĐ
ĢŧĢĻ3ĢĐ![]() ŧō3
ŧō3![]() Đ6
Đ6
Ąū―âÎöĄŋ
ĢĻ1ĢĐ°Ņ![]() šÍĩã
šÍĩã![]() īúČëÅŨÎïÏßĩÄ―âÎöĘ―ĢŽÁз―ģĖŨéĢŽŋÉĩÃ―áÂÛĢŧ
īúČëÅŨÎïÏßĩÄ―âÎöĘ―ĢŽÁз―ģĖŨéĢŽŋÉĩÃ―áÂÛĢŧ
ĢĻ2ĢĐČįÍž1ĢŽļųūÝķÔģÆĩÄÐÔÖĘĩÃ![]() ĢŽŋÉĩÃ
ĢŽŋÉĩÃ![]() ĢŽÉč
ĢŽÉč![]() ĢŽÔō
ĢŽÔō![]() ĢŽÔÚ
ĢŽÔÚ![]() ÖÐĢŽļųūÝđīđÉķĻĀíĩÃ
ÖÐĢŽļųūÝđīđÉķĻĀíĩÃ![]() ĢŽÁз―ģĖŋÉĩÃ―áÂÛĢŧ
ĢŽÁз―ģĖŋÉĩÃ―áÂÛĢŧ
ĢĻ3ĢĐ·ÖÁ―ÖÖĮéŋöĢšÏČËĩÃũ![]() ĘĮÖą―ĮČý―ĮÐÎĢŽËųŌÔ
ĘĮÖą―ĮČý―ĮÐÎĢŽËųŌÔ![]() ŌēĘĮÖą―ĮČý―ĮÐÎĢŽļųūÝ
ŌēĘĮÖą―ĮČý―ĮÐÎĢŽļųūÝ![]() ĢŽŧÍžĢŽÓÉđīđÉķĻĀíÁз―ģĖŋÉ―âīðĢŪ
ĢŽŧÍžĢŽÓÉđīđÉķĻĀíÁз―ģĖŋÉ―âīðĢŪ
―âĢšĢĻ1ĢĐ![]() ÅŨÎïÏß
ÅŨÎïÏß![]() đýĩã
đýĩã![]() šÍĩã
šÍĩã![]() ĢŽ
ĢŽ
![]()
![]() ĢŽ
ĢŽ
―âĩÃ ĢŽ
ĢŽ
![]()
![]() Ģŧ
Ģŧ
ĢĻ2ĢĐČįÍž1ĢŽÁŽ―Ó![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
![]() ĩã
ĩã![]() đØÓÚÖąÏß
đØÓÚÖąÏß![]() ĩÄķÔģÆĩã
ĩÄķÔģÆĩã![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]()
![]() Óë
Óë![]() Öá―ŧÓÚĩã
Öá―ŧÓÚĩã![]() ĢŽÓë
ĢŽÓë![]() Öá―ŧÓÚĩã
Öá―ŧÓÚĩã![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĩã
ĩã![]() ĢŽ
ĢŽ
ÉčÖąÏß![]() Óë
Óë![]() Öá―ŧÓÚĩã
Öá―ŧÓÚĩã![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ

Éč![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ
ÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]()
![]() ĢŽ
ĢŽ
![]() ÖąÏß
ÖąÏß![]() ĩÄ―ØūāΊ
ĩÄ―ØūāΊ![]() Ģŧ
Ģŧ
ĢĻ3ĢĐ![]() ĩã
ĩã![]() ĘĮ
ĘĮ![]() ÖáÕý°ëÖáÉÏŌŧĩãĢŽ
ÖáÕý°ëÖáÉÏŌŧĩãĢŽ
![]() ĘĮÖą―ĮČý―ĮÐÎĢŽĮŌ
ĘĮÖą―ĮČý―ĮÐÎĢŽĮŌ![]()
ĩą![]() Óë
Óë![]() ČŦĩČĘąĢŽīæÔÚÁ―ÖÖĮéŋöĢš
ČŦĩČĘąĢŽīæÔÚÁ―ÖÖĮéŋöĢš
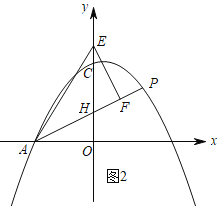
ĒŲČįÍž2ĢŽĩą![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
ÓÉĢĻ2ĢĐÖŠĢš![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
―âĩÃĢš![]() ŧō
ŧō![]() ĢĻÉá
ĢĻÉá![]() ĢŽ
ĢŽ
![]() ĩã
ĩã![]() ĩÄŨÝŨøąęĘĮ
ĩÄŨÝŨøąęĘĮ![]() Ģŧ
Ģŧ
ĒÚČįÍž3ĢŽĩą![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ

![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
![]() ÖÐĢŽÓÉđīđÉķĻĀíĩÃĢš
ÖÐĢŽÓÉđīđÉķĻĀíĩÃĢš![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
―âĩÃĢš![]() ĢŽ
ĢŽ
![]() ĩã
ĩã![]() ĩÄŨÝŨøąęĘĮ
ĩÄŨÝŨøąęĘĮ![]() Ģŧ
Ģŧ
ŨÛÉÏĢŽĩã![]() ĩÄŨÝŨøąęĘĮ
ĩÄŨÝŨøąęĘĮ![]() ŧō
ŧō![]() ĢŪ
ĢŪ

 ÆßēĘĖâŋĻŋÚËãÓĶÓÃŌŧĩãÍĻÏĩÁÐīð°ļ
ÆßēĘĖâŋĻŋÚËãÓĶÓÃŌŧĩãÍĻÏĩÁÐīð°ļ