题目内容
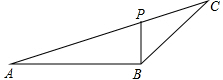
如图,在△ABC中,∠ABC=135°,点P为AC上一点,且∠PBA=90°,
=
.
(1)求tan∠APB的值;
(2)若PB=2,求AC的长度.
| CP |
| PA |
| 1 |
| 2 |
(1)求tan∠APB的值;
(2)若PB=2,求AC的长度.

(1)过点P作PD∥AB交BC于点D,
∵tan∠PBD=tan45°=1,
∴PB=PD,∵
=
,
∴tan∠APB=
=
=
=3;
(2)由(1)得:∵PB=2,
∴AB=6,
∴AP=
=2
,
∴AC=
AP=3
.

∵tan∠PBD=tan45°=1,
∴PB=PD,∵
| CP |
| PA |
| 1 |
| 2 |
∴tan∠APB=
| AB |
| PB |
| AB |
| PD |
| AC |
| PC |
(2)由(1)得:∵PB=2,
∴AB=6,
∴AP=
| 62+22 |
| 10 |
∴AC=
| 3 |
| 2 |
| 10 |


练习册系列答案
相关题目